Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1
a) trước tiên chứng minh\(\widehat{ABM}=\widehat{ACN}\)
rồi mới chứng minh 2 tam giác ABM và ACN bằng nhau
suy ra AM = AN
b)Đầu tiên chứng minh\(\widehat{ABH}=\widehat{ACK}\)
rồi chứng minh hai tam giác ABH và ACK bằng nhau
suy ra BH = CK
c) vì hai tam giác ABH và ACK bằng nhau (cmt)
nên AH = AK
d) ta có \(\widehat{AMB}=\widehat{ACN}\)(hai tam giác ABH và ACK bằng nhau)
nên dễ cm \(\widehat{MBH}=\widehat{NCK}\)
còn lại tự cm
e) dễ cm tam giác ABC đều
vẽ \(BH\perp AC\)
nên BH vừa là đường cao; phân giác và trung tuyến
dễ cm \(\Delta BHC=\Delta NKC\)
nên \(\widehat{BCH}=\widehat{NCK}=60^0\)
từ đó dễ cm AMN cân và OBC dều

A B C M N O H K 1 2 1 2
Cm: a) Ta có: góc ABC + góc ABM = 1800 (kề bù)
góc ACN + góc ACB = 1800 (kề bù)
và góc ABC = góc ACB (vì t/giác ABC cân tạo A)
=> góc ABM = góc ACN
Xét t/giác ABM và t/giác ACN
có AB = AC (gt)
góc ABM = góc ACN (cmt)
BM = CN (gt)
=> t/giác ABM = t/giác ACN (c.g.c)
b) ko đề
c) Xét t/giác AHB và t/giác AKC
có góc H1 = góc K1 = 900 (gt)
AB = AC (gt)
góc HAB = góc KAC (vì t/giác ABM = t/giác ACN)
=> t/giác AHB = t/giác AKC (ch - gn)
=> AH = AK (hai cạnh tương ứng)
Xét t/giác AHO và t/giác AKO
có AH = AK (cmt)
góc H1 = góc K1 = 900 (gt)
AO : chung
=> t/giác AHO = t/giác AKO (ch - cgv)
=> HO = KO(hai cạnh tương ứng)
Mà HB + BO = HO
KC + CO = OK
và HB = KC (vì t/giác AHB = t/giác AKC)
=> BO = CO
=> t/giác OBC là t/giác cân tại O

Bài 6:
a: Xét ΔBAC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: \(AH=\sqrt{AB^2-BH^2}=4.8\left(cm\right)\)

Hình như bài này là bai 71,72 gì đó ở SGK 7ở gần cuối trang thì phải

a)Xét tam giác ABM và tam giác CAN có:
BM=CN(gt)
AB=AC(do tam giác ABC cân)
\(\widehat{B}=\widehat{C}\)(tam giác ABC cân)
Suy ra \(\Delta ABM=\Delta CAN\)(c.g.c)
Tgiac ABC cân tại A => AB = AC, góc ABC = ACB
a) góc ABC = ACB => góc ABM = ACN (góc kề bù)
Xét tgiac ABM và ACN có:
+ BM = CN
+ góc ABM =ACN (cmt)
+ AB = AC
=> Tgiac ABM = ACN (c-g-c)
=> đpcm
b) Do tgiac ABM = ACN (cmt) nên góc BAM = CAN (2 góc t/ứng)
Xét tgiac AHB và AKC có:
+ AB = AC
+ góc AHB = AKC = 90 độ
+ góc ABM = CAN
=> Tgiac AHB = AKC (ch-gn)
=> AH = AK (2 cạnh t/ứng)
=> đpcm
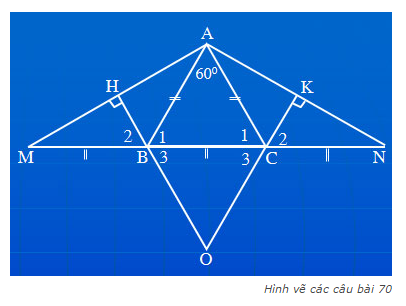
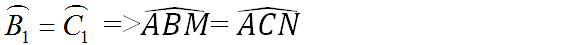
A B C M N H K O a)Ta có:
△ABC cân tại A⇒\(\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow180^0-\widehat{ABC}=180^0-\widehat{ACB}\)
\(\Rightarrow\widehat{ABM}=\widehat{ACN}\)
Xét △ABM và △ACN có:
AB=AC (gt)
\(\widehat{ABM}=\widehat{ACN}\) (cmt)
BM=CN (gt)
⇒△ABM = △ACN (cgc)
b)Từ △ABM = △ACN (câu a)
⇒\(\widehat{AMB}=\widehat{ANC}\)(2 góc tương ứng) hay \(\widehat{HMB}=\widehat{KNC}\)
Xét △CKN vuông tại K và △BHM vuông tại H, ta có:
CN=BM (gt)
\(\widehat{KNC}=\widehat{HMB}\) (cmt)
⇒△CKN= △BHM (cạnh huyền- góc nhọn)
⇒CK=BH (2 cạnh tương ứng)
Xét △CKA vuông tại K và △BHA vuông tại H, ta có:
AC=AB (gt)
CK=BH (cmt)
⇒△CKA= △BHA (cạnh huyền- cạnh góc vuông)
⇒KA=HA (2 cạnh tương ứng)
c)Từ △CKN= △BHM (câu b)
⇒\(\widehat{NCK}=\widehat{MBH}\) (2 góc tương ứng)
Mà \(\widehat{NCK}=\widehat{BCO}\)(đối đỉnh); \(\widehat{MBH}=\widehat{CBO}\)(đối đỉnh)
⇒\(\widehat{BCO}=\widehat{CBO}\) ⇒△OBC cân tại O
d)△ABM = △ACN (câu a) ⇒AM=AN (2 cạnh tương ứng)
⇒△AMN cân tại A
\(\widehat{MAN}=70^0\Rightarrow\widehat{ANM}=\widehat{AMN}=\frac{180^0-\widehat{MAN}}{2}=\frac{180^0-70^0}{2}=\frac{110^0}{2}=55^0\)
\(\Rightarrow\widehat{NCK}=\widehat{MBH}=180^0-\left(90^0+55^0\right)=180^0-145^0=35^0\Rightarrow\widehat{OCB}=\widehat{OBC}=35^0\Rightarrow\widehat{BOC}=110^0\)