Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔBAC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
b) Xét ΔAMD và ΔCMH có
MA=MC(gt)
\(\widehat{AMD}=\widehat{CMH}\)(hai góc đối đỉnh)
MD=MH(gt)
Do đó: ΔAMD=ΔCMH(c-g-c)
Suy ra: AD=HC(Hai cạnh tương ứng)
c) Ta có: ΔAMD=ΔCMH(cmt)
nên \(\widehat{MAD}=\widehat{MCH}\)(hai góc tương ứng)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//HC(Dấu hiệu nhận biết hai đường thẳng song song)
hay AD//HB
Xét tứ giác ABHD có
AD//BH(cmt)
AD=BH(=HC)
Do đó: ABHD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: AB//DH(Hai cạnh đối)

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔAHC
Suy ra: BH=CH
hay H là trung điểm của BC
b: Xét ΔABH vuông tại H và ΔDCH vuông tại H có
HB=HC
HA=HD
Do đó: ΔABH=ΔDCH
c: Ta có: ΔABH=ΔDCH
nên AB=DC
mà AB=AC
nên DC=AC
hay ΔACD cân tại C

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét tứ giác ABKH có
I là trung điểm chung của AK và BH
=>ABKH là hbh
=>BK//AH
=>BK vuông góc BC
c: KB=AH
AH<AB
=>KB<AB
d: Xét ΔBCK có CH/CB=CM/CK
nên HM//BK
=>HM vuông góc BC
mà AH vuông góc BC
nên A,H,M thẳng hàng

a, Xét tg AHB và tg AHC, có:
AB=AC(tg cân)
góc AHB= góc AHC(=90o)
AH chung.
=>tg AHB= tg AHC( ch-cgv)
=>BH=HC.
=>H là trung điểm của BC.

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
b: Sửa đề: Trên tia đối của tia HA
Xét ΔABH vuông tại H và ΔDCH vuông tại H có
HA=HD
HB=HC
Do đó: ΔABH=ΔDCH
c: Sửa đề: Cm ΔACD cân
Ta có: ΔABH=ΔDCH
=>DC=AB
mà AB=AC
nên CA=CD
=>ΔCAD cân tại C

a: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
Do đo ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
=>AC//BD
c: Xét ΔAHB vuông tại H và ΔDKC vuông tại K có
AB=DC
góc ABH=góc DCK
Do đo: ΔAHB=ΔDKC
=>AH=DK và BK=CH

Thấy cái ý △AMN cân với cái chứng minh BAC = 1/2 MAN cũng ko lên quan lắm. Tham khảo qua ạ tại câu b hơi có vấn đề :(
a) Xét △AHB và △AHC có:
AHB = AHC (= 90o)
AH: chung
AB = AC (△ABC cân)
=> △AHB = △AHC (ch-cgv)
b) Xét △ADM và △ADH có:
ADM = ADH (= 90o)
DM = DH (gt)
AD: chung
=> △ADM = △ADH (2cgv)
=> AM = AH (2 cạnh tương ứng) (1)
Xét △ANE và △AHE có:
AEH = AEN (= 90o)
EH = EN (gt)
AE: chung
=> △ANE = △AHE (2cgv)
=> AN = AH (hai cạnh tương ứng) (2)
Từ (1) và (2) => AM = AN => △AMN cân tại A
Ta có: MAN = MAB + BAH + HAC + CAN
Mà MAB = HAB, HAC = CAN (suy ra được từ các tam giác bằng nhau)
=> MAN = 2BAH + 2 HAC
=> MAN = 2BAC
=> BAC = 1/2MAN
c) Ta có: HAD = HAE (△AHB = △AHC)
Mà HAD = DAM, HAE = EAN
=> HAD + DAM = HAE + EAN
=> HAM = HAN
Gọi giao điểm AH và MN là F
Xét △AFM và △AFN có:
AF: chung
FAM = FAN (cmt)
AM = AN (cmt)
=> △AFM = △AFN (c.g.c)
=> AFM = AFN (2 góc tương ứng)
Mà AFM + AFN = 180o => AFM = AFN = 90o
=> AH vuông góc MN (1)
Gọi giao điểm của DE và AH là I
Xét △ADH và △AEH có:
ADH = AEH (= 90o)
AH: chung
HAD = HAE (△HAB = △HAC)
=> △ADH = △AEH (ch-gn)
=> AD = AE (2 cạnh tương ứng)
Xét △AID và △AIE có:
AI: chung
IAD = IAE (cmt)
AD = AE (cmt)
=> △AID = △AIE (c.g.c)
=> AID = AIE (2 góc tương ứng)
Mà AID + AIE = 180o => AID = AIE = 90o
=> AH vuông góc DE (2)
Từ (1) và (2) => MN // DE
d) \(\Delta\)ABC cân tại A có AH là đường cao
=> AH là đường trung tuyến
=> H là trung điểm BC
=> BH = HC = BC : 2 = 3 ( cm )
\(\Delta\)ABH vuông tại H => AB2 - BH2 = AH2 => AH = 4 cm
=> S ( \(\Delta\)ABH ) = \(\frac{1}{2}\)BH . AH =\(\frac{1}{2}\) HD . AB
=> 3.4 = HD . 5 => HD = 2,4 cm
\(\Delta\)BDH vuông tại D => BD2 = BH2 - HD2 = 3,24 => BD = 1,8 cm
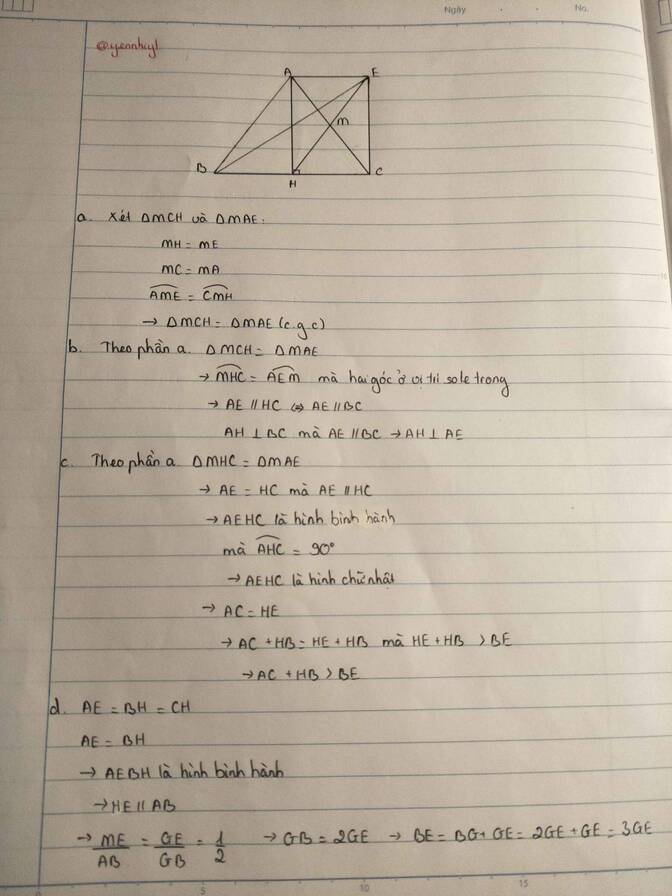
a) Xét tg ABH và ACH có :
AB=AC (tg ABC cân A)
AH-chung
\(\widehat{AHB}=\widehat{AHC}=90^o\)
=> Tg ABH=ACH (ch-cgv)
b) Xét tg ADM và CHM có :
AM=MC (gt)
HM=MD (gt)
\(\widehat{AMD}=\widehat{HMC}\left(đđ\right)\)
=> Tg ADM=CHM (c.g.c)
=> AD=HC (đccm)
c) Do tg ADM=CHM
\(\Rightarrow\widehat{ADM}=\widehat{MHC}\)
=> AD//BC
Lại có : \(\widehat{ADM}=\widehat{ABC}\left(=\widehat{ACB}\right)\)
=> AB//DH
#H