K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
5
3 tháng 3 2018
Vì tam giác ABC cân tại A có góc A bằng 61 độ nên :
\(\widehat{ABC}=\widehat{ACB}=\frac{180^o-61^o}{2}=59,5^o\)
Ta thấy góc A bằng 61 độ và góc C bằng 59,5 độ nên góc A > góc C
Do đó BC > AB ( cạnh đối diện với góc lớn hơn thì lớn hơn )
Vậy BC > AB
LB
1
20 tháng 2 2022
Bài 1:
AC=4cm
Xét ΔABC có AB<AC
nên \(\widehat{C}< \widehat{B}\)
Bài 2:
BC=6cm
=>AB+AC=14cm
mà AB=AC
nên AB=AC=7cm
Xét ΔABC có AB=AC>BC
nên \(\widehat{B}=\widehat{C}>\widehat{A}\)
PT
2
P
25 tháng 2 2022
_Xét △ABC ta có:
\(\widehat{A}\) + \(\widehat{B}\) + \(\widehat{C}\) = 180o
=> 50o + \(\widehat{B}\) + \(\widehat{C}\) = 180o
=> \(\widehat{B}\) + \(\widehat{C}\) = 180o \(-\) 50o
=> \(\widehat{B}\) + \(\widehat{C}\) = 130o : 2 = 65o
=> \(\widehat{B}\) = \(\widehat{C}\) = 65o
=> \(\widehat{A}\) < \(\widehat{B}\) => BC < AB
Vậy trong △ABC có:
BC < AB
10 tháng 4 2022
Xét ΔDBH vuông tại D và ΔECH vuông tại E có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔDBH=ΔECH
Suy ra: HD=HE
mà HE<HC
nên HD<HC
22 tháng 2 2022
Bài 1:
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB>AC
nên BD>CD
23 tháng 6 2023
a: \(AB=\sqrt{6^2+8^2}=10\left(cm\right)\)
BH<AH<AB
=>góc HAB<góc HBA<góc AHB
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
c: góc KAH=góc HAC
góc KHA=góc HAC
=>góc KAH=góc KHA
=>ΔAKH cân tại K
Xét ΔABC có
H là trung điểm của BC
HK//AC
=>K là trung điểm của AB
DD
1
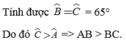
tùy trường hợp thôi