Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình bn tự vẽ nha
a, Xét hai tam giác vuông AME và AMF có :
AM là cạnh chung
\(\widehat{EAM} = \widehat{FAM}\) ( do AM là tia phân giác góc A )
=> tam giác AME = tam giác AMF ( cạnh huyền - góc nhọn )
=> ME = MF ( hai cạnh tương ứng )
b,Do AC // BM
mà IF vuông góc CA
=> FI vuông góc với BI ( tính chất đường vuông góc )
Do ME vuông góc AB
MI vuông góc BI
=> AB // BI ( tính chất hai đường thẳng // )
Xét hai tam giác vuông MEB và MIB có
BM là cạnh chung
\(\widehat{EMB} = \widehat{MBI}\) ( hai góc so le trong )
=> tam giác MEB = tam giác MIB ( cạnh huyền - góc nhọn )
=> BE = Bi ( hai cạnh tương ứng )

tu ve hinh :
a; b, xet tamgiac AMF va tamgiac AME co : AM chung
goc AFM = goc AEM = 90 do MF | AC va ME | AB (gt)
goc FAM = goc EAM do AM la phan giac cua goc BAC (gt)
=> tamgiac AMF = tamgiac AME (ch - gn)
=> AE = AF (dn) (1)
AB = AC do tamgiac ABC can tai A (gt)
AE + EB = AB
AF + FC = AC
=> EB = FC
xet tamgiac BEM va tamgiac CFM co : goc B = goc C do tamgiac ABC can tai A (gt)
goc MEB = goc MFC do ...
=> tamgiac BEM = tamgiac CFM (cgv - gnk)
=> MB = MC
c, (1) => tamgiac AEF can tai E (dn)
=> goc AEF = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc B = (180 - goc BAC) : 2
=> goc AEF = goc B ma 2 goc nay dong vi
=> EF // BC (dh)
Giải
Bạn tự vẽ hình
a; b, Xét \(\Delta AMF\) va \(\Delta AME\) có : AM chung
\(\widehat{AFM}=\widehat{AEM}=90^0\) do MF\(\perp\)AC va ME\(\perp\)AB
\(\widehat{FAM}=\widehat{EAM}\)do AM la phân giác của \(\widehat{BAC}\)
\(\Rightarrow\Delta AFM=\Delta AME\)
\(\Rightarrow AE=AF\) (1)
AB = AC do \(\Delta ABC\) cân tại A
AE + EB = AB
AF + FC = AC
\(\Rightarrow\) EB = FC
Xét \(\Delta BEM\) và \(\Delta CFM\) có : \(\widehat{B}\) = \(\widehat{C}\) do \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{MEB}=\widehat{MFC}\)
\(\Rightarrow\Delta BEM=\Delta CFM\)
\(\Rightarrow\) MB = MC
c, Từ (1) suy ra \(\Delta AEF\)cân tại E
\(\Rightarrow\widehat{AEF}=\left(180-\widehat{BAC}\right)\div2\)
\(\Delta ABC\) cân tại A \(\Rightarrow\)\(\widehat{B}\)= (180 - \(\widehat{BAC}\)) : 2
\(\Rightarrow\widehat{AEF}=\widehat{B}\) mà hai góc này đồng vị
\(\Rightarrow EF//BC\)

xét 2 tam giác ABM=tam giác ACM(c.c.c)(tự cm)
nên góc AMB=góc AMC=180ddooj /2=90 độ
suy ra AM vuông góc vs BC
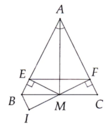
a: Xét ΔAFM vuông tại F và ΔAEM vuông tại E có
AM chung
\(\widehat{FAM}=\widehat{EAM}\)
Do đó: ΔAFM=ΔAEM
Suy ra: ME=MF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC