Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C I O K M N J H E F D x
Gọi E là điểm đối xứng với A qua đường thẳng OI. Tia AI cắt (O) tại D khác A. DE giao BC tại F.
Ta thấy \(\Delta\)MIN và \(\Delta\)AIE cân tại I có ^IMN = ^IAE (Vì MN // AE vuông góc OI) => ^MIN = ^AIE => I,N,E thẳng hàng.
=> MN là đường trung bình \(\Delta\)AIE => AE = 2.MN, IE = 2.IN
Ta có: AE // IK (Cùng vuông góc OI) => ^KIE = ^IEA = ^IAE = ^BAE - ^BAD = ^BDx - ^DBC = ^BFD = ^KFE
=> Tứ giác KEIF nội tiếp => ^KEI = ^BFI (1)
Mặt khác: \(\Delta\)DFC ~ \(\Delta\)DCE (g.g) => DC2 = DF.DE => DI2 = DF.DE => \(\Delta\)DFI ~ \(\Delta\)DIE (c.g.c)
=> ^DFI = ^DIE = 2.^IAE = 2.^BFD (Vì ^IAE = ^BFD) => ^KIE = ^BFI (2)
Từ (1) và (2) => ^KIE = ^KEI => \(\Delta\)IKE cân tại K. Từ đó: \(\Delta\)IKE ~ \(\Delta\)AIE (g.g) => IE2 = IK.AE
Dễ thấy MJ là đường trung bình \(\Delta\)AIK => IK = 2.MJ. Kết hợp với AE = 2.MN (cmt)
Suy ra: IE2 = 4.MJ.MN hay AI2 = 4.MJ.MN => 4.MA2 = 4.MJ.MN => MA2 = MJ.MN => \(\Delta\)MJA ~ \(\Delta\)MAN (c.g.c)
=> ^MJA = ^MAN. Tương tự thì ^MJI = ^MIN => ^MJA + ^MJI = ^MAN + ^MIN => ^AJI = 1800 - ^ANI
Lại có: H là trực tâm \(\Delta\)AIN => ^AHI = 1800 - ^ANI. Do đó: ^AHI = ^AJI => Tứ giác AIHJ nội tiếp
=> ^AJH + ^AIH = 1800 <=> ^MJA + ^MJH + 900 - ^IAN = ^MJH + 900 = 1800 => ^MJH = 900
=> JH vuông góc MN. Mà OI cũng vuông góc MN nên JH // OI (đpcm).

Do K đối xứng với D qua trung điểm của BC nên ta có
\(BD=CK,BK=CD\)
Dựng đường kính DF của (I). Theo hình , thì ta được ba điểm A, F , K thẳng hàng
ta có\(\widehat{KDL}=\widehat{DIC}\left(=90^0-\widehat{CID}\right)=>\)tam giác IDC = tam giác DKL (g.g), từ đó suy ra
\(\frac{DF}{DK}=\frac{2ID}{DK}=\frac{2DC}{KL}=\frac{KB}{KN}\)
=> tam giác DFK = tam giác KBN (c.g.c)
zì zậy nên : \(\widehat{KNB}=\widehat{DKF}=90^0-\widehat{NKF}\)
=>\(\widehat{KNB}+\widehat{NKF}=90^0,\)do đó \(AK\perp BN\)

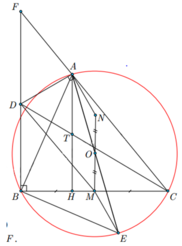
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
K O C A B I H 1 1
Xét tam giác ABO vuông tại B và ACO vuông tại C
có: AB=AC , AO chung
=> \(\Delta ABO=\Delta ACO\)
=> BO=CO
Xét tam giác DBC có: BO=CO=KO
=> Tam giác KBC vuông tại B
=> KB vuông góc với CI
Xét tam giác IKC vuông tại K có KB là dường cao
=> \(BK^2=IB.BC\Rightarrow\frac{BK}{IB}=\frac{BC}{BK}\)(1)
Ta có tam giác OBK vuông cân tại O và tam giác ABC cân tại A
=> \(\widehat{ABC}=\widehat{ACB};\widehat{OBK}=\widehat{OKB}\)(2)
mà \(\widehat{OBK}+\widehat{OBC}=\widehat{CBK}=90^o=\widehat{ABO}=\widehat{ABC}+\widehat{OBC}\)
=> \(\widehat{OBK}=\widehat{ABC}\)(3)
Từ (2) và (3) suy ra : \(\frac{AB}{BO}=\frac{BC}{BK}\)(4)
Từ (1) và (4)
=> \(\frac{BK}{BI}=\frac{AB}{BO}\)
Xét tam giác IBO và tam giác KBA có:
\(\frac{BK}{BI}=\frac{AB}{BO}\)( chứng minh trên)
\(\widehat{IBO}=\widehat{KBA}\)( vì \(\widehat{IBK}=\widehat{OBA}=90^o\))
=> \(\Delta IBO~\Delta KBA\)
=> \(\widehat{A_1}=\widehat{O_1}\)
Gọi giao điểm của IO và AK là H
=> \(\widehat{BAH}=\widehat{BOH}\)
=> BAOH nội tiếp
=> \(\widehat{OHA}=\widehat{OBA}=90^o\)
( Nếu chua học nội tiếp em hãy xét hai tam giác đồng dạng)
=> IO vuông AK