Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kéo dài AD cắt đường tròn ngoại tiếp ABC tại H'.
Đặt x=HD;
Vì góc BAC nhọn và do H' đối xứng với H qua BC nên ta có: DH'=HD=x; CH'=CH=30
Áp dụng Pitago cho tg vuông ACH':
AC^2+(CH')^2=(AH')^2 -->AC^2+900=(14+2x)^2 (*)
Mặt khác CD^2= AD.DH' --> CD^2=(14+x).x (**)
trừ 2 vế (*) và (**):
AC^2+900-CD^2 =(14+2x)^2 -(14+x).x (***)
Mà AC^2-CD^2 =AD^2 =(14+x)^2;
Thế vào (***) ta được ph.tr:
(14+x)^2+900 =(14+2x)^2-(14+x)x ---> x^2+7x-450=0
phtr trên có nghiệm x= -25 (loại) và x= 18 (nhận)
AD= 14+x =14+18= 32 cm

Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
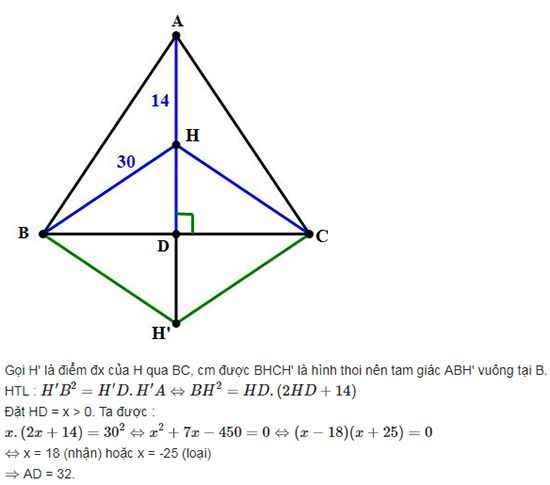
Gọi H' đối xứng với H qua BC, D là giao điểm của AH và BC.
Dễ thấy BHCH' là hình thoi.
\(\Rightarrow\Delta ABH'\)vuông tại B
\(\Rightarrow H'B^2=H'D.H'A\)
\(\Leftrightarrow BH^2=HD\left(2HD+14\right)\)
\(\Leftrightarrow30^2=HD\left(2HD+14\right)\)
\(\Leftrightarrow\orbr{\begin{cases}HD=18\\HD=-25\left(l\right)\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}AD=14+18=32\\BD=\sqrt{30^2-18^2}=24\end{cases}}\)
\(\Rightarrow AB=\sqrt{32^2+24^2}=40\)
mình không biết làm