Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :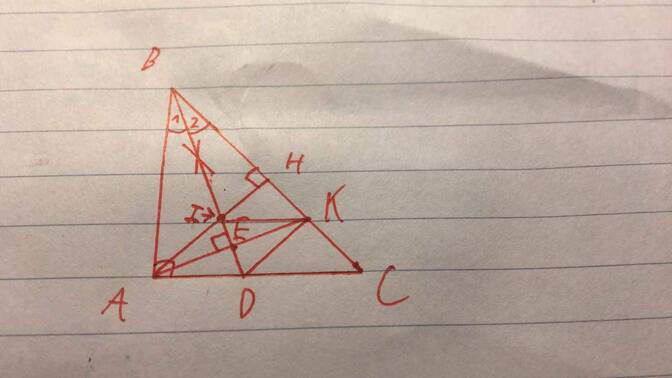

a: Xét ΔBAK có
BE là đường cao
BE là đường trung tuyến
Do đó: ΔBAK cân tại B
b: Xét ΔBAD và ΔBKD có
BA=BK
\(\widehat{ABD}=\widehat{KBD}\)
BD chung
Do đó: ΔBAD=ΔBKD
Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)

Em tham khảo tại đây nhé.
Câu hỏi của Bảo Trân Nguyễn Hoàng - Toán lớp 7 - Học toán với OnlineMath
b) Xét tam giác vuông ACB và tam giác vuông BDA có:
Cạnh AB chung
\(\widehat{ABC}=\widehat{BAD}\left(=30^o\right)\)
\(\Rightarrow\Delta ACB=\Delta BDA\) (Cạnh huyền góc nhọn)
\(\Rightarrow AD=BC\)

Bạn tự vẽ hình
a Xét tam giác ABD và tam giác ACE có
góc BEC= góc CDB= 90 độ
AB=AC
AH chung
suy ra tam giác ABD= tam giác ACE(c.g.c)
b) Vì tam giác ABD= tam giác ACE( theo a)
suy ra BD=CEhay BH=CH( 2canhj tương ứng)
Xét tam giác BHC có
BH= CH
suy ra tam giác BHC cân tại H

A B D E K C H I
a.Xét hai tam giác vuông ABE và tam giác vuông KBE có
góc ABE = góc KBE = 90độ
cạnh BE chung
góc ABE = góc KBE [ gt ]
Do đó ; tam giác ABE = tam giác KBE [ g.c.g ]
\(\Rightarrow\) AB = KB [ cạnh tương ứng ]
Vậy tam giác ABK cân tại B
b.Xét tam giác ABD và tam giác KBD có
AB = KB [ vì tam giác ABE = tam giác KBE theo câu a ]
góc ABD = góc KBD [ vì BD là tia phân giác góc B ]
cạnh BD chung
Do đó ; tam giác ABD = tam giác KBD [ c.g.c ]
\(\Rightarrow\)góc BAD = góc BKD [ góc tương ứng ]
mà bài cho góc BAD = 90độ nên góc KBD = 90độ
Vậy DK vuông góc với BC
c.Vì DK vuông góc với BC và AH vuông góc với BC nên
DK // AH
Suy ra ; góc HAK = góc DKA [ ở vị trí so le trong ] [ 1 ]
Mặt khác ; AD = DK [ vì tam giác ABD = tam giác KBD ]
\(\Rightarrow\)tam giác ADK là tam giác cân tại D nên
góc DKA = góc DAK [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra
góc HAK = góc DAK
Vậy AK là tia pg góc KAD hay AK là tia pg góc HAC
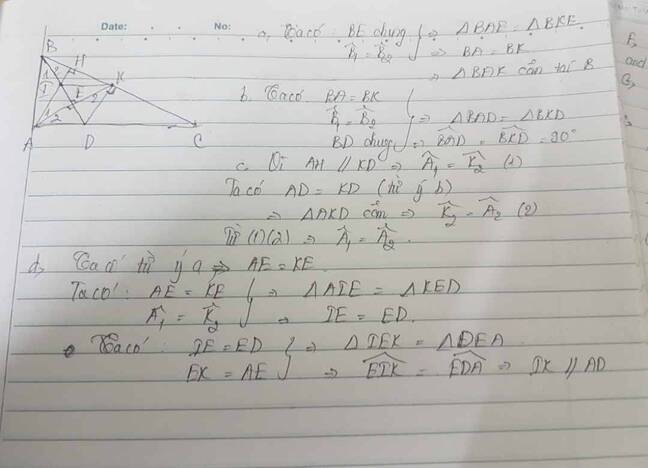
a/ Xét \(\Delta ABD\left(D=1v\right)\) và \(\Delta ACE\left(E=1v\right)\) có:
góc A chung (gt)
AB = AC (\(\Delta ABC\) cân tại A)
=> \(\Delta ABD=\Delta ACE\) (ch-gn)
b/ Xét\(\Delta ABK\left(K=1v\right)\) và \(\Delta ACK\left(K=1v\right)\) có:
AB = AC (\(\Delta ABC\) cân tại A)
AK chung (gt)
=> \(\Delta ABK=\Delta ACK\) (ch-cgv)
=> góc BAK = góc CAK (hai góc tương ứng)
=> AK là tia phân giác của góc BAC
giải hộ mik nhanh nhất có thể ạ