Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) Xét tam giác ABE và tam giác ACF có:
Góc AEB=góc AFC(=90 độ)
Góc A chung
=>Tam giác ABE đồng dạng vs tam giác ACF (g-g)
b)
Vì tam giác ABE đồng dạng vs tam giác ACF(cmt)
=>\(\frac{AB}{AC}=\frac{AE}{AF}\)
Xét tam giác AFE và tam giác ACB có:
Góc A chung(gt)
\(\frac{AB}{AC}=\frac{AE}{AF}\)
=>Tam giác AFE và tam giác ACB đồng dạng (c-g-c)
c)
H ở đou ra vại? :))

a: Xét ΔBHI vuông tại H và ΔAKI vuông tại K có
góc BIH=góc AIK
=>ΔBHI đồng dạng vói ΔAKI
=>IB*IK=IA*IH
b: góc BHA=góc BKA=90 độ
=>BHKA nội tiếp
=>góc BAH=góc BKH

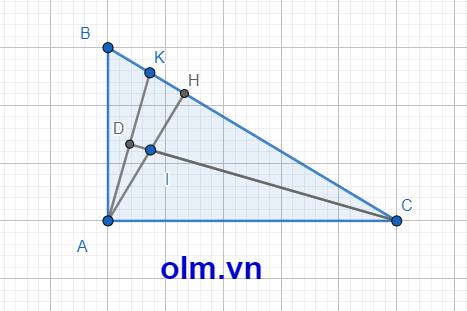
Xét \(\Delta\) HBA và \(\Delta\) ABC có \(\widehat{H}\) = \(\widehat{A}\) = 900; \(\widehat{B}\) chung
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) ABC (g-g)
Tương tự ta có: \(\Delta\) HAC \(\sim\) \(\Delta\) ABC (g-g-g)
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) HAC ( t/c hai tam giác đồng dạng)
⇒ \(\dfrac{HB}{HA}\) = \(\dfrac{HA}{HC}\) = \(\dfrac{BA}{AC}\)( theo khái niệm của tam giác đồng dạng.)
Mặt khác: KI là đường trung bình của tam giác ABH nên:
\(\dfrac{HI}{HA}\) = \(\dfrac{HK}{HB}\) ⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HB}{HA}\)
⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HA}{HC}\) mà \(\widehat{AHK}\) = \(\widehat{CHI}\) = 900
⇒ \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ( c-g-c)
b, Kéo dài CI cắt AK tại D ta có:
vì \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ⇒ \(\widehat{HAK}\) = \(\widehat{HCI}\)
Xét \(\Delta\) HAK và \(\Delta\) DCK có: \(\widehat{A}\) = \(\widehat{C}\) ( cmt)
\(\widehat{K}\) chung
⇒ \(\Delta\) HAK \(\sim\) \(\Delta\) DCK ( g-g)
⇒ \(\widehat{H}\) = \(\widehat{D}\)= 900 ⇒ AK \(\perp\) CI tại D ( đpcm)

a: Xét ΔAHI vuông tại H và ΔACH vuông tại H có
góc HAI chung
=>ΔAHI đồng dạng với ΔACH
Xét ΔAHI vuông tại Ivà ΔHCI vuông tại I có
góc HAI=góc CHI
=>ΔAHI đồng dạng với ΔHCI
b: Xet ΔIHC có IM/IH=IK/IC
nên MK//HC
=>MK vuông góc AH
Xet ΔAHK có
KM,HI là đường cao
KM cắt HI tại M
=>M là trực tâm
=>AM vuông góc HK tại N
=>MN là đường cao của ΔHMK

a: HC vuông góc AI
IH vuông góc HM
=>góc AIH=góc MHC(1)
góc IAH=90 độ-góc ABD
góc HCM=90 độ-góc FBC
=>góc IAH=góc HCM(2)
Từ (1), (2) suy ra ΔAHI đồng dạng với ΔCMH
b: Kẻ CG//IK(G thuộc AB), CG cắt AD tại N
=>HM vuông góc CN
=>M là trựctâm của ΔHCN
=>NM vuông góc CH
=>NM//AB
=>NM//BG
=>N là trung điểm của CG
IK//GC
=>IH/GN=HK/NC
mà GN=NC
nên IH=HK
=>H là trung điểm của IK

A B C H K I E F
Xét \(\Delta BAC\) Và \(\Delta ACH\) có :
\(\widehat{BAC}\)\(=\)\(\widehat{AHC}\) ( cùng = 900 )
\(\widehat{C}\)là góc chung
\(\Rightarrow\) \(\Delta BAC\)\(~\)\(\Delta AHC\) ( g - g ) (1)
\(\Rightarrow\)\(\frac{BC}{AC}=\frac{AB}{AH}\)\(\Rightarrow BC.AH=AB.AC\)
b) Xét \(\Delta AHC\)có :
K là trung điểm của CH
I là trung điểm của AH
\(\Rightarrow\)IK // AC
Do IK // AC :
\(\Rightarrow\)\(\Delta HIK\)\(~\)\(\Delta HAC\) (2)
Từ (1) và (2) =) \(\Delta HIK\)\(~\)\(\Delta ABC\)
Do \(HE\)\(\perp\)\(AB\)\(\Rightarrow\)\(\widehat{A\text{E}H}\)= 900
\(HF\)\(\perp\)\(AC\)\(\Rightarrow\)\(\widehat{FHE}\)= 900
Xét tứ giác AEHF có:
\(\widehat{BAC}=\widehat{A\text{E}H}=\widehat{FHE}\)\(=90^0\)
\(\Rightarrow\)AEHF là hình chữ nhật \(\Rightarrow\) AE = HF
Xét \(\Delta ABC\)\(\perp\)tại \(A\)
Áp dụng định lí py - ta - go
BC2 = AB2 + AC2
52 = 32 + AC2
AC2 = 16
AC = 4 ( cm )
Ta có ; \(S_{\Delta ABC}\)\(=\frac{AB.AC}{2}\)\(=\frac{3.4}{2}=6\)cm2
\(S_{\Delta ABC}=\frac{1}{2}.BC.AH\)\(=\frac{1}{2}.5.AH=2,5.AH\)
\(\Rightarrow2,5.AH=6\)\(\Rightarrow AH=2,4\)cm
Xét \(\Delta AHC\)\(\perp\)tại A
Áp dụng định lí py - ta - go
AC2 = AH2 + HC2
42 = (2,4)2 + CH2
CH2 = 10,24
CH = 3,2 cm
Ta có : \(S_{\Delta AHC}=\frac{AH.AC}{2}=\)\(\frac{2,4.3,2}{2}=3,84\)cm2
\(S_{\Delta AHC}=\frac{1}{2}.AC.HF\)\(=\frac{1}{2}.4.HF=2.HF\)
\(\Rightarrow\)2.HF = 3.84
HF = 1.92 cm
\(\Rightarrow A\text{E}=1,92\)( Vì HF = AE , cmt)

A B C M H I K N a) Ta có : góc HCB = góc BAH (1) vì cùng phụ với góc ABH
Dễ thấy góc HMB = góc IHN (cùng phụ với góc MHN)
Mà góc AHB + góc BHI = góc HMC + góc HMB = 1800
=> góc HMC = góc AHI (2)
Từ (1) và (2) suy ra đpcm