Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

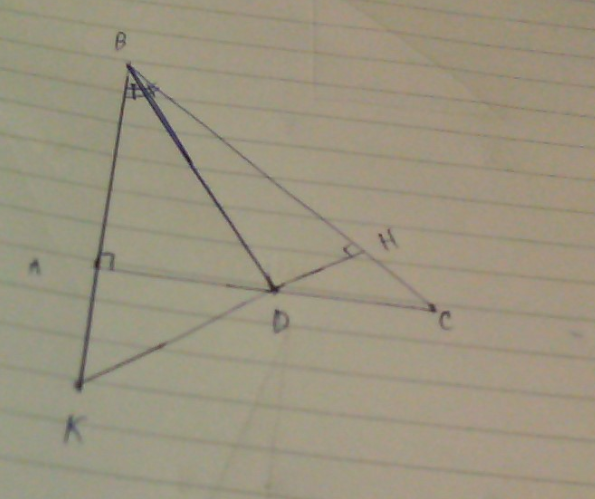
Xét \(\triangle ABD\) vuông tại \(A\) và \(\triangle HBD\) vuông tại H \(( DH \bot BC)\) ta có :
\(\widehat{ABD}=\widehat{HBD}\) ( tia phân giác của \(\widehat{ABC}\) cắt \(AC\) tại \(D\) )
Chung \(BD\)
\(\Rightarrow\) \(\triangle ABD\) \(=\) \(\triangle HBD\) ( ch - gn )
\(\Rightarrow AB = BH\) ( \(2\) cạnh tương ứng ) (1)
Do \(\begin{cases} \widehat{BAD} = 90^o\\ \widehat{BHD} = 90^0\end{cases}\)
\(\Rightarrow \widehat{KAD} = \widehat{CHD} = 90^o\)
Xét \(\triangle AKD\) vuông tại \(A\) và \(\triangle HCD\) vuông tại \(H\) ta có :
\(\widehat{ADK} = \widehat{HDC}\) ( \(2\) góc đối đỉnh )
\(AD=DH \) ( \(\triangle ABD = \) \(\triangle HBD\) )
\(\Rightarrow\) \(\triangle AKD=\) \(\triangle HCD\) ( cgv - gnk )
\(\Rightarrow AK = CH\) ( \(2\) cạnh tương ứng ) (2)
Từ (1) và (2)
\(\Rightarrow AB+AK = BH+CH\)
\(\Leftrightarrow BK=BC\)
\(\Rightarrow \triangle KBC\) cân tại \(B\)

a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
=>ΔAHD=ΔAED
b: DH=DE
DE<DC
=>DH<DC
c: Xét ΔAKC có
CH,KE là đường cao
CH căt KE tại D
=>D là trực tâm
=>AD vuông góc KC

5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D

Bài 4: a) Xét ABE vàHBE có:
BE chung
ABE= EBH (vì BE là phân giác)
=> ABE=HBE (cạnh huyền- góc nhọn)
b, Vì ABE=HBE(cmt)
=> BA = BH và EA = EH
=> điểm B, E cách đều 2 mút của đoạn thẳng AH
=>BE là đường trung trực của đoạn thẳng AH
c, Vì AC vuông góc BK => EAK = \(90\) độ
EH vuông góc BC => EHC = 90 độ
Xét AEK vàHEC có:
EAK = EHC (= 90độ)(cmt)
AE = EH (cmt)
AEK = HEC (đối đỉnh)
=> AEK HEC (g.c.g)
=> EK = EC (2 cạnh tương ứng)
Xét HEC vuông tại H (vì EHC = 90 độ )
có EH < EC(cạnh huyền lớn hơn cạnh góc vuông)
Mà AE = EH (cmt) => AE < EC

Bạn tự vẽ hình nha!!!
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.

a) Xét tam giác DAB và tam giác DHB:
góc DAB= góc DHB =90o
DB chung
góc DBA= góc DBH
=> tam giác DAB = tam giác DHB (cạnh huyền _góc nhọn)
=> DA=DH (2 cạnh tương ứng)
b)
Ta có: DA = DH (cmt) (1)
và trong tam giác CHD :
DH là cạnh góc vuông
DC là cạnh huyền
=> DH < DC (2)
Từ (1) và (2) => AD < DH
c) Xét tam giác DAK và tam giác DHC:
góc DAK = góc DHC = 90o
DA = DH (cmt)
góc KDA = góc CDH (đối đỉnh)
=> tam giác DAK = tam giác DHC (cạnh góc vuông_ góc nhọn)
=> AK = HC (2 cạnh tương ứng)
Ta có: AB = HB (do tam giác DAB = tam giác DHB)
và AK = HC (cmt)
mà BK = AB + AK
BC = HB + HC
=> BK = BC
=> tam giác KBC cân
Cô nêu cách trình bày khác của câu c nhé. :)
Xét tam giác KBC, có KH, CK là các đường cao nên D là trực tâm của tam giác KBC. Từ đó suy ra BD là đường cao của tam giác KBC. Mà BD lại là đường phân giác nên tam giác KBC cân tại B.

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.