Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tự kẻ hình nha
a) vì tam giác ABC cân A=> AB=AC
xét tam giác ABM và tam giác ACM có
A1=A2(gt)
AB=AC(cmt)
AM chung
=> tam giác ABM= tam giác ACM(cgc)
=> AMB=AMC(hai góc tương ứng)
mà AMB+AMC=180 độ( kề bù)
=> AMB=AMC=180/2=90 độ=> AM vuông góc với BC
b) từ tam giác AMB= tam giác AMC=> BM=CM( hai cạnh tương ứng)
=> M là trung điểm BC=> AM là trung tuyến
BQ là trung tuyến
mà AM giao BQ tại G=> G là trọng tâm của tam giác ABC
c) ta có BC=BM+CM mà BM=CM=> BM=CM=BC/2=18/2=9 cm
ta có AM^2=AB^2-BM^2=15^2-9^2=225-81=144=12^2=> AM=12
vì G là trọng tâm của tam giác ABC=> AG=2/3AM=> AG=12*2/3=8 cm
d) vì MD//AC=> CAM=AMD( so le trong)
mà CAM=BAM(gt)
=> BAM=AMD=> tam giác AMD cân D=> AD=DM
vì tam giác ABM vuông tại M=> ABM+BAM=90 độ=> ABM=90 độ-BAM
vì AMD+DMB=AMB=> DMB=90 độ-AMD
mà AMD=BAM (cmt)
=> DMB=ABM=> tam giác DMB cân D=> BD=DM=> BD=AD=> D là trung điểm AB=> DC là trung tuyến
mà G là trọng tâm => G thuộc CD=> D, G, C thẳng hàng

Vì tam giác \(ABC\)đều nên trung trực của \(AC\)cũng là trung tuyến của \(AC\)nên \(O\)là trọng tâm của tam giác \(ABC\)
Suy ra \(OA=\frac{2}{3}AM\).
Tam giác \(ABC\)đều nên \(AM\perp BC\).
Theo định lí Pythagore:
\(AC^2=AM^2+MC^2\)
\(\Leftrightarrow AM^2=AC^2-MC^2=10^2-5^2=75\)
\(\Leftrightarrow AM=5\sqrt{3}\left(cm\right)\).
\(OA=\frac{2}{3}AM=\frac{10\sqrt{3}}{3}\left(cm\right)\).

A B C M 1 2 Q G
A) XÉT \(\Delta ABM\)VÀ\(\Delta ACM\)CÓ
\(AB=AC\left(GT\right)\)
\(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
AM LÀ CẠNH CHUNG
=>\(\Delta ABM\)=\(\Delta ACM\)( C-G-C)
TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ ĐƯỜNG CAO
=> AM LÀ ĐƯỜNG CAO CỦA \(\Delta ABC\)
\(\Rightarrow AM\perp BC\)
B) TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ TRUNG TUYẾN
=> AM LÀ TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ABC\)
MÀ BG LÀ ĐƯỜNG TRUNG TUYẾN THỨ HAI CỦA \(\Delta ABC\)
HAI ĐƯỜNG TRUNG TUYẾN NÀY CẮT NHAU TẠI G
\(\Rightarrow G\)LÀ TRỌNG TÂM CỦA \(\Delta ABC\)
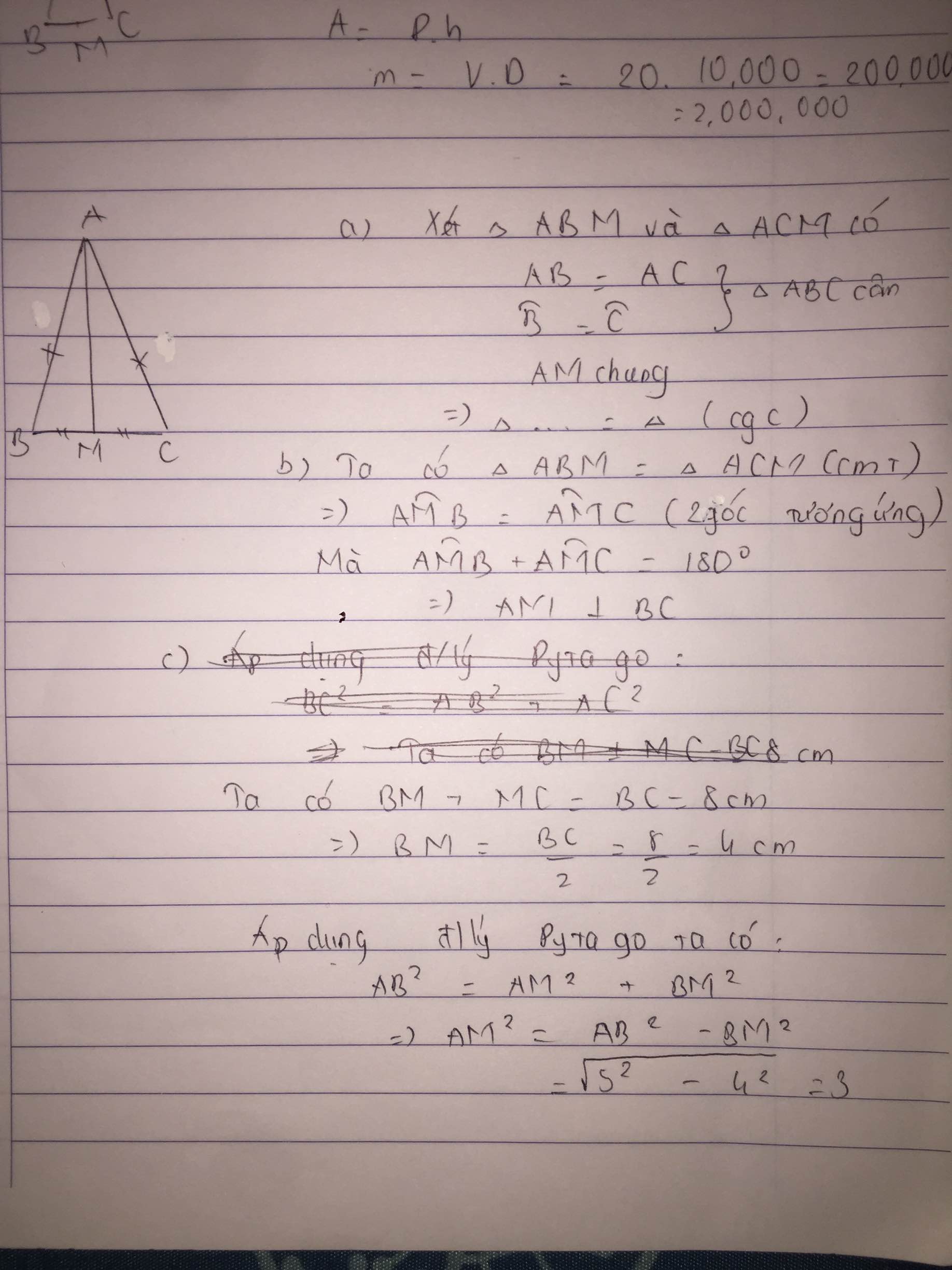
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
\(BM=\sqrt{AB^2-AM^2}=6\left(cm\right)\)
vì ABC cân tại A => AB=AC,B=C
mà AB=10cm=>AC=10cm
AB^2=AM^2+BM^2
10^2=8^2+BM^2
100=64+BM^2
BM^2=100-64
BM^2=36
=>BM=6 cm