Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha!
do AN=AM=>Tam giác AMN cân
do tam giác ABC cân \(\Rightarrow\widehat{B}=\widehat{C}=\frac{180-\widehat{A}}{2}=\frac{180-100}{2}=40\)
và tam giác AMN cân \(\Rightarrow\widehat{M}=\widehat{N}=\frac{180-\widehat{A}}{2}=\frac{180-100}{2}=40\)
do \(\widehat{M}=\widehat{B}\)
do hai góc đồng vị =>MN//BC

Vì tam giác ABC cân tại A nên \(\widehat{A}=\widehat{B}\)
\(\Rightarrow\widehat{B}=\frac{180^o-\widehat{A}}{2}\)
= \(\frac{180^o-100^o}{2}=40^o\) ( 1 )
Mà AM = AN ( gt ) nên \(\Delta AMN\) cân tại A \(\Rightarrow\widehat{AMN}=\widehat{ANM}\)
\(\Rightarrow\widehat{AMN}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-100^o}{2}=40^o\) ( 2)
Từ ( 1 ) và ( 2 ) \(\Rightarrow\widehat{B}=\widehat{AMN}\)
Vậy \(MN//BC\) ( vì có cặp góc ở vị trí đồng vị bằng nhau )
Chúc bạn học tốt !!!

Vì \(\Delta ABC\)là tam giác cân tại A
=> \(\widehat{B}=\widehat{C}\)( hai góc ở đáy )
=> \(\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-100^0=80^0\)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{80^0}{2}=40^0\)
Xét \(\Delta AMN\)có \(AM=AN\)
=> \(\Delta AMN\)là tam giác cân tại A
=> \(\widehat{M}_1=\widehat{N}\)( hai góc ở đáy )
Lại có : \(\widehat{M_1}+\widehat{N}=180^0-\widehat{A}=180^0-100^0=80^0\)
=> \(\widehat{M_1}=\widehat{N}=\frac{80^0}{2}=40^0\)
Ta có : \(\widehat{M_1}+\widehat{M_2}=180^0\)( kề bù )
=> \(\widehat{M_2}=180^0-\widehat{M_1}=180^0-40^0=140^0\)
Ta có : \(\widehat{B}+\widehat{M_2}=40^0+140^0=180^0\)( 1 )
mà \(\widehat{B}\)và \(\widehat{M_2}\)ở vị trí trong cùng phía ( 2 )
Từ ( 1 ) và ( 2 ) => \(MN//BC\)( đpcm )

a) +Xét tam giác ABC cân tại A có \(\widehat{A}\)= 100o
=>\(\widehat{B}=\widehat{C}=40^o\)
TT ta có: Tam giác AMN cân(AM=AN) tại A có\(\widehat{A}\)=100o
=>\(\widehat{AMN}=\widehat{ANM}=40^o\)
=>\(\widehat{B}=\widehat{C}\)\(=\widehat{AMN}=\widehat{ANM}\)
=>\(\widehat{B}=\widehat{AMN}\)
Mà hai góc này đồng vị =>MN//BC
+Xét tam giác AMC và tam giác ANB có:
AM=AN
 chung
AC=AB
Do đó tam giác AMC= tam giác ANB(c.g.c)
Suy ra BN=CM(hai cạnh t.ứ)
Bài 2 để tí mik lm tiếp, mik đag bận, bạn tích mik để mik có cái để tl tiếp nhé
Chúc học tốt

tam giac ABC can tai A=>goc B=180-100/2=40(1)
ta co AN+NC=AC
AM+MB=AB
ma AM=AN,AB=AC
=>NC=BM=>tam giac AMN can tai A
tam giac AMN can tai A=>goc M=180-100/2=40(2)
tu (1)(2)=.B=M ma hai goc nay o vi tri dong vi =>MNsog sog BC (tick nha)

(*) Vì AM = AN nên ΔAMN cân tại A
=> góc AMN = ANM ( 2 góc đáy)
mà AMN + ANM = 180 - BAC => AMN = (180 - BAC) :2 (1)
Do ΔABC cân tại A nên góc ABC = ACB hay MBC = NCB
mà góc ABC + ACB = 180 - BAC => ABC = (180 - BAC ) : 2 (2)
Từ (1) và (2) suy ra AMN = ABC
do 2 góc này ở vị trí so le trong nên MN // BC → đpcm
(*) Ta có: AM + MB = AB
AN + NC = AC
mà AM = AN; AB = AC => MB = NC
Xét ΔBMC và ΔCNB có:
BM = CN (cm trên)
góc MBC = NCB (cm trên)
BC chung
=> ΔBMC = ΔCNB (c.g.c)
=> MC = NB (2 cạnh tương ứng) → đpcm
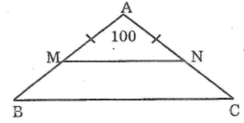

Tam giác ABC cân tại A nên \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}=\frac{180^0-100^0}{2}=40^0\)
AM = AN => \(\Delta AMN\)cân tại A nên \(\widehat{AMN}=\frac{180^0-\widehat{A}}{2}=\frac{180^0-100^0}{2}=40^0\)
Hai đường thẳng MN và BC tạo với cát tuyến AB hai góc đồng vị bằng nhau \(\widehat{AMN}=\widehat{B}=40^0\)nên MN//BC.