Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
CB chung
góc EBC=góc DCB
=>ΔEBC=ΔDCB
b: Xét ΔHBC có góc HCB=góc HBC
nên ΔHBC cân tại H
c: Xet ΔABH và ΔACH có
AB=AC
BH=CH
AH chung
=>ΔABH=ΔACH
=>góc BAH=góc CAH
=>AH làphân giác của góc BAC

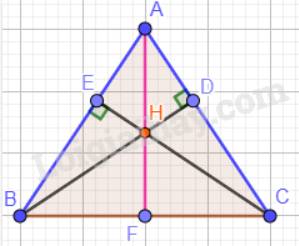
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.

Bạn tự vẽ hình ik nha
a. Xét tam giác ABD và tam giác ACE có:
góc D = góc E = 90* (gt)
AB = AC (gt)
góc A chung
=> tg ABD = tg ACE (c. huyền-g. nhọn)
b. Vì H là giao điểm của 2 dường cao BD và CE
Nên AH cũng là đường cao cùa tg ABC hay AH vuông góc BC
Do tg ABC là tam giác cân => AI là đường cao đồng thời cũng là dường trung tuyến => BI = CI => I là trung điểm của BC
c.Ta có: góc ACE = góc ABD (doc tg ABD = tg ACE)
và góc ABC = góc ACB
=> góc DBC = góc ECB
Ta có: BD vuông góc AC (gt)
CF vuông góc AC (gt)
=> CF song song BD (2 dường thẳng cùng vuông góc với 1 dường thẳng)
=> góc DBC = góc BCF ( so le trong)
Mà góc DBC = góc ECB
=> góc ECB = góc BCF
=> BC lá tia phân giác của góc ECF

a, Xét ∆ ABD và ∆ ACE có:
Góc D = góc E = 90°
AB = AC (∆ ABC cân)
Góc BAC chung
➡️∆ ABD = ∆ ACE (ch-gn)
➡️AD = AE (2 cạnh t/ư)
b, ✳️C/m AH là tia phân giác của góc BAC
Xét∆ ABC cân tại A có:
BD vuông góc với AC
CE vuông góc với AB
H là giao điểm của BD và CE
➡️H là trực tâm ∆ ABC
➡️AH vuông góc với BC
mà ∆ ABC cân tại A
➡️AH là đg cao đồng thời là đg phân giác
➡️AH là p/g góc BAC(đpcm)
✳️C/m AH là đg trung trực của ED
Xét ∆ AED cân tại A (AD = AE)
➡️AH là đg phân giác đồng thời là đg trung trực
➡️AH là đg trung trực của ED (đpcm)
c, Xét ∆ AEH và ∆ ADH có:
AE = AD (cmt)
Góc BAH = góc CAH (cmt)
AH chung
➡️∆ AEH = ∆ ADH (c.g.c)
➡️HE = HD (2 cạnh t/ư)
Xét ∆ CDH vuông tại D
➡️CH > HD
mà HE = HD (cmt)
➡️CH > HE
Còn câu d để mk nghĩ đã nhé
Câu d nè bn.
d, Vì AH là đg trung trực của EF và AH vuông góc với BC
➡️ED // BC (quan hệ từ vuông góc đến song song)
Ta có: góc FED = góc DBC (2 góc có 2 cạnh tương ứng song song)
Gọi AH giao BC tại M
Xét ∆ ABC cân tại A
➡️AH là đg cao đồng thời là trung tuyến
HM là trung tuyến của BC
Xét ∆ IBC có HM là đg cao đồng thời là trung tuyến
➡️∆ IBC cân tại I
➡️Góc DBC = góc ECB
Mà góc ECB = góc DEC (2 góc so le trong)
➡️Góc DEC = góc DBC
mà góc DBC = góc FED (cmt)
➡️Góc FED = góc DEC
➡️ED là tia phân giác góc FEC
Xét ∆ FEC có: CI là phân giác góc DCE (gt)
EI là phân giác góc FEC (cmt)
CI và EI giao nhau tại I
➡️I là tâm đg tròn nội tiếp∆ FEC
➡️FI là phân giác góc CFE
mà góc CFE vuông (EF // BD, góc BDC = 90°)
➡️Góc EFI = góc CFI = 90° ÷ 2 = 45°
Vậy góc EFI = 45°
Hok tốt nhé~

bạn cm AM là trung tuyến
đồng thời dựa vào tam giác ABC cân và AH là đường cao ta cm được AH là trung tuyến
suy ra AM trùng với AH
vậy A,H,M thẳng hàng

a/ Xét \(\Delta ABD\left(D=1v\right)\) và \(\Delta ACE\left(E=1v\right)\) có:
góc A chung (gt)
AB = AC (\(\Delta ABC\) cân tại A)
=> \(\Delta ABD=\Delta ACE\) (ch-gn)
b/ Xét\(\Delta ABK\left(K=1v\right)\) và \(\Delta ACK\left(K=1v\right)\) có:
AB = AC (\(\Delta ABC\) cân tại A)
AK chung (gt)
=> \(\Delta ABK=\Delta ACK\) (ch-cgv)
=> góc BAK = góc CAK (hai góc tương ứng)
=> AK là tia phân giác của góc BAC

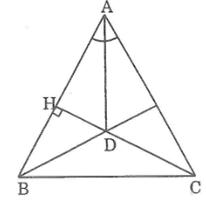
Chú ý H là trực tâm tam giác ABC, từ đó AH vừa là đường cao vừa là đường phân giác