Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
Do \(\Delta ABC\) cân\(\widehat{ABC}=\widehat{ACB}\)
\(\widehat{DBC}+\widehat{ABC}=\widehat{DCB}+\widehat{ACB}=90^o\Rightarrow\widehat{DBC}=\widehat{DCB}\Rightarrow\Delta BDC\) cân tại D
b/
Ta có \(\Delta BDC\) cân nên\(BD=CD\)
\(\Delta ABC\) cân nên \(AB=AC\)
\(\Rightarrow\Delta ABD=\Delta ACD\) (Hai tg vuông có các cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{BAD}=\widehat{CAD};\widehat{BDA}=\widehat{CDA}\) => AD là phân giác của \(\widehat{A}\) và \(\widehat{D}\)
c/
Do tg ABC cân tại A và AD là phân giác \(\widehat{A}\) nên AD là đường cao đồng thời là đường trung tuyến thuộc cạnh BC của tg ABC (Trong tg cân đường phân giác đồng thời là đường cao, đường trung tuyến và đường trung trực)
\(\Rightarrow AD\perp BC\) và đi qua trung điểm của BC

C1: Xét \(\Delta ABD\) và \(\Delta ACD\) có:
AD (chung)
\(\widehat{ADB}=\widehat{ADC}\) ( = 900)
AB = AC ( \(\Delta ABC\)cân tại A )
Do đó: \(\Delta ABD=\Delta ACD\) (cạnh huyền - cạnh góc vuông)

a, Xét tam giác ADB và tam giác ADC có
AD _ chung ; ^DAB = ^DAC ; AB = AC
Vậy tam giác ADB = tam giác ADC (c.g.c)
b, Xét tam giác ABC cân tại A có AD là phân giác
đồng thời là đường cao hay AD vuông BC
c, Xét tam giác AMD và tam giác AND có
AD _ chung ; ^MAD = ^NAD
Vậy tam giác AMD = tam giác AND ( ch-gn )
=> AM = AN ( 2 cạnh tương ứng )
d, Ta có AM/AB = AN/AC => MN // BC ( Ta lét đảo )

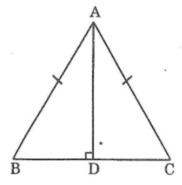
Xét hai tam giác vuông ADB và ADC, ta có:
∠(ADB) =∠(ADC) = 90o
AB = AC (giả thiết)
AD cạnh chung
Suy ra: ΔADB= ΔADC(cạnh huyền, cạnh góc vuông)
⇒ ∠(BAD) =∠(CAD) (hai góc tương ứng)
Vậy AD là tia phân giác ∠(BAC)

xét 2 tam giác vuông BAD và CAD có :AD : cạnh chungAB = AC ( vì tam giác ABC cân tại A )=> tam giác BAD = tam giác CAD ( cạnh huyền - cạnh góc vuông)=> ^BAD = ^CAD ( 2 góc tương ứng )=> AD là tia phân giác của góc A
mik ko vẽ hình đc trên đây nên mik chỉ có lời giải
hình nhờ bạn tự vẽ giúp mik
mik cảm ơn

cau a phai la tamgiac HBA = tamgiac AMD phai k
phai thi tu ve hinh :
a, DM | IH (GT) va AH | BH (GT) ma 2 duong thang DM; BH phan biet
=> DM // BH (dl)
=> goc MDB + DBH = 180o (tcp)
co tamgiac ADB vuong can tai A do goc A = 90o (gt) va AD = AB (gt)
=> goc MDA + goc ABH = 90o
ma goc MDA + goc DAM = 90o (tc) do tamgiac DMA vuong tai M do DM | IA (gt)
=> goc MAD = goc ABH
xet tamgiac AMD va tamgiac BHA co : goc DMA = goc ANB = 90o va AD = AB (GT)
=> tamgiac AMD = tamgiac BHA (ch - gn)
Xét tam giác ABD và tam giác ACD có
góc D1= góc D2 (=90 độ)
góc B = góc C (vì tam giác ABC cân ở A)
AB=AC(vì tam giác ABC cân ở A)
=> Tam giác ABD= Tam giác ACD(c h- g n)
=> Góc BAD= góc CAD( hai góc tg ứng)
=>AD là tia pg của góc A (dpcm)
((mk vẽ hình hơi xấu thông cảm nhé))
Mong bạn sẽ tích cho mình
