Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé
a) Ta có: \(IN=\frac{1}{3}NC\)và
\(IC=\frac{2}{3}NC\Leftrightarrow IK=\frac{IC}{2}=\frac{2}{3}NC\cdot\frac{1}{2}=\frac{1}{3}NC\)
\(\Rightarrow IN=IK\)(1)
Mặt khác \(IM=\frac{1}{3}BM\)và
\(IB=\frac{2}{3}BM\Leftrightarrow HI=\frac{IB}{2}=\frac{2}{3}BM\cdot\frac{1}{2}=\frac{1}{3}BM\)
\(\Rightarrow IM=IH\)(2)
Từ (1) và (2) => tứ giác MNHK là hbh. (3)
b) Từ (3) => Nếu BM_|_ CN thì tứ giác MNHK là hình thoi (4)
c) Để MNHK là hcn thì NK = HM hay IN = IM <=> NC=BM <=> tam giác ABC cân tại A
d) Từ (4) và c) => Để MNHK là hình vuông thì tam giác ABC cân tại A và BM _|_ CN

a: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC và \(NM=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
H là trung điểm của GB
K là trung điểm của GC
Do đó: HK là đường trung bình của ΔGBC
Suy ra: HK//BC và \(HK=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra NM//HK và NM=HK
hay NMKH là hình bình hành

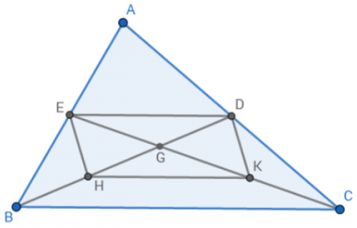
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi


1)
Xét ΔABC có
N là trung điểm của AB(do CN là đường trung tuyến)
M là trung điểm của AC(do BM là đường trung tuyến)
Do đó: NM là đường trung bình của ΔABC(định nghĩa đường trung bình của tam giác)
⇒NM//BC và \(NM=\frac{BC}{2}\)(định lí 2 về đường trung bình của tam giác)(1)
Xét ΔIBC có
H là trung điểm của IB(gt)
K là trung điểm của IC(gt)
Do đó: HK là đường trung bình của ΔIBC(định nghĩa đường trung bình của tam giác)
⇒HK//BC và \(HK=\frac{BC}{2}\)(định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra HK//NM và HK=NM
Xét tứ giác NMKH có HK//NM(cmt) và HK=NM(cmt)
nên NMKH là hình bình hành(dấu hiệu nhận biết hình bình hành)
2:
Nếu BM⊥CN thì
HM⊥NK
Xét hình bình hành NMKH có HM⊥NK(cmt)
nên NMKH là hình thoi(dấu hiệu nhận biết hình thoi)
Vậy: Khi hai đường trung tuyến BM và CN vuông góc với nhau thì tứ giác MNHK là hình thoi
Thanks bn nhiều