
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

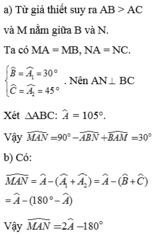


Sửa câu b: Từ M kẻ ME
Bg
a/ Xét hai tam giác AMB và AMC có:
AB = AC (gt)
BM = MC (vì M là trung điểm của BC)
AM là cạnh chung
Nên \(\Delta AMB=\Delta AMC\)(c.c.c)
Vậy \(\Delta AMB=\Delta AMC\)
b/ Xét hai tam giác vuông AME và AMF có:
\(\widehat{EAM}=\widehat{FAM}\)(vì \(\Delta AMB=\Delta AMC\))
AM là cạnh chung
Nên \(\Delta AME=\Delta AMF\)(g.c.g)
Do đó AE = AF (hai cạnh tương ứng)
Vậy AE = AF
c và d hơi dài. Đợi một thời gian :((

a) c/m tam giác BMI =CMI (c. g. c)
=>BM=CM(hai cạnh tương ứng)
Xét tam giác BMC có BM=CM (cmt)
=> tam giác BMC cân tại M
b) Xét tam giác ABC có
Góc BAC + gócABC+ góc ACB =180 độ
=>góc ABC=60 độ
Ta lại cos tam giác BMC cân tại M =>gocs MBC=góc C =30 độ
Mà góc ABC =ABM+CBM
=>CBM=ABM=30 độ =1/2ABC
Vậy BM là phân giác của góc ABC
c) c/m tam giác ABM= tam giác ibm( cạnh huyền canh góc vuông)
=> AB=BI
MÀ BI=1/2BC=>AB=1/2BC
d) c/m tam giác BKI=BCA( c. g. c)
=> góc KIB=góc CAB=90 độ
=> KI vuông góc với BC
mà MI cũng vuoong góc với BC
=>3 điểm K,M,I thẳng hàng

a/ Xét tam giác BEM và tam giác CFM có:
góc BEM = góc CFM = 900 (GT)
BM = MC (AM là trung tuyến t/g ABC)
góc B = góc C (t/g ABC cân)
=> tam giác BEM = tam giác CFM
b/ Ta có: AB = AC (t/g ABC cân)
BE = CF (t/g BEM = t/g CFM)
=> AE = AF
Xét hai tam giác vuông AEM và AFM có:
AE = AF (cmt)
AM: cạnh chung
=> tam giác AEM = tam giác AFM
=> ME = MF
Ta có: AE = AF; ME = MF
=> AM là trung trực của EF
c/ Xét hai tam giác vuông ABD và ACD có:
AB = AC (GT)
AD: cạnh chung
=> tam giác ABD = tam giác ACD
=> BD = CD
Ta có: AB = AC; BD = CD
=> AD là trung trực của EF
Ta có: AM là trung trực của EF
AD là trung trực của EF
=> AM trùng AD
Vậy A;M;D thẳng hàng.
---> đpcm.