Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác ABM và ACM có AB=AC (gt), BM = CM(gt) và AM chung nên 2 tam giác bằng nhau (c.c.c)
b) Tam giác ABC cân tại A có AM là đường trung tuyến nên đồng thời là đường cao kẻ từ A => AM \(\perp\)BC
c) Tam giác EBC và FCB có
EB = FC
\(\widehat{EBC}=\widehat{FCB}\) (tam giác ABC cân tại A)
BC chung
=> tam giác EBC = tam giác FCB (c.g.c)
d) tam giác EBC = tam giác FCB => \(\widehat{ICB}=\widehat{IBC}\) (2 góc tương ứng)
=> tam giác IBC cân tại I => IB = IC
Xét tam giác AIB và AIC có
AI chung
AB =AC (gt)
IB=IC
=> tam giác AIB = AIC (c.c.c)
=> \(\widehat{BAI}=\widehat{CAI}\) mà \(\widehat{BAI}+\widehat{CAI}=\widehat{BAC}\)
=> AI là tia phân giác của \(\widehat{BAC}\) (1)
Tam giác ABC cân tại A có AM là đường trung tuyến => đồng thơi là đường pgiac
=> AM là tia pgiac của \(\widehat{BAC}\) (2)
từ 1 và 2 => A,I,M thẳng hàng
e) Có AB = AC(gt) => AE + EB = AF + FC mà BE = CF => AE = AF => tam giác AEF cân tại A
=> \(\widehat{AEF}=\widehat{AFE}=\dfrac{180^o-\widehat{EAF}}{2}=\dfrac{180^o-\widehat{BAC}}{2}\) (3)
Tam giác ABC cân tại A => \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^o-\widehat{BAC}}{2}\)(4)
Từ 3 + 4 => \(\widehat{AEF}=\widehat{ABC}\) mà 2 góc đồng vị => EF // AB
a. vì AB=AC => tam giác ABC là tam giác cân
Xét tam giác ABC ta có :
AB=AC (gt)
AM cạnh chung
BM=CM (tam giác ABC là tam giác cân)
=> tam giác ABM = tam giác ACM ( c.c.c )
b. ta có : AB=AC ; BM=CM
=> AM vuông góc BC

a: Xét ΔAFB và ΔAEC có
AF=AE
góc BAF chung
AB=AC
Do đo: ΔAFB=ΔAEC
Suy ra FB=EC
b: Xét ΔGCB có góc GCB=góc GBC
nên ΔGBC cân tại G
c: Xét ΔABC có AE/AB=AF/AC
nên FE//BC

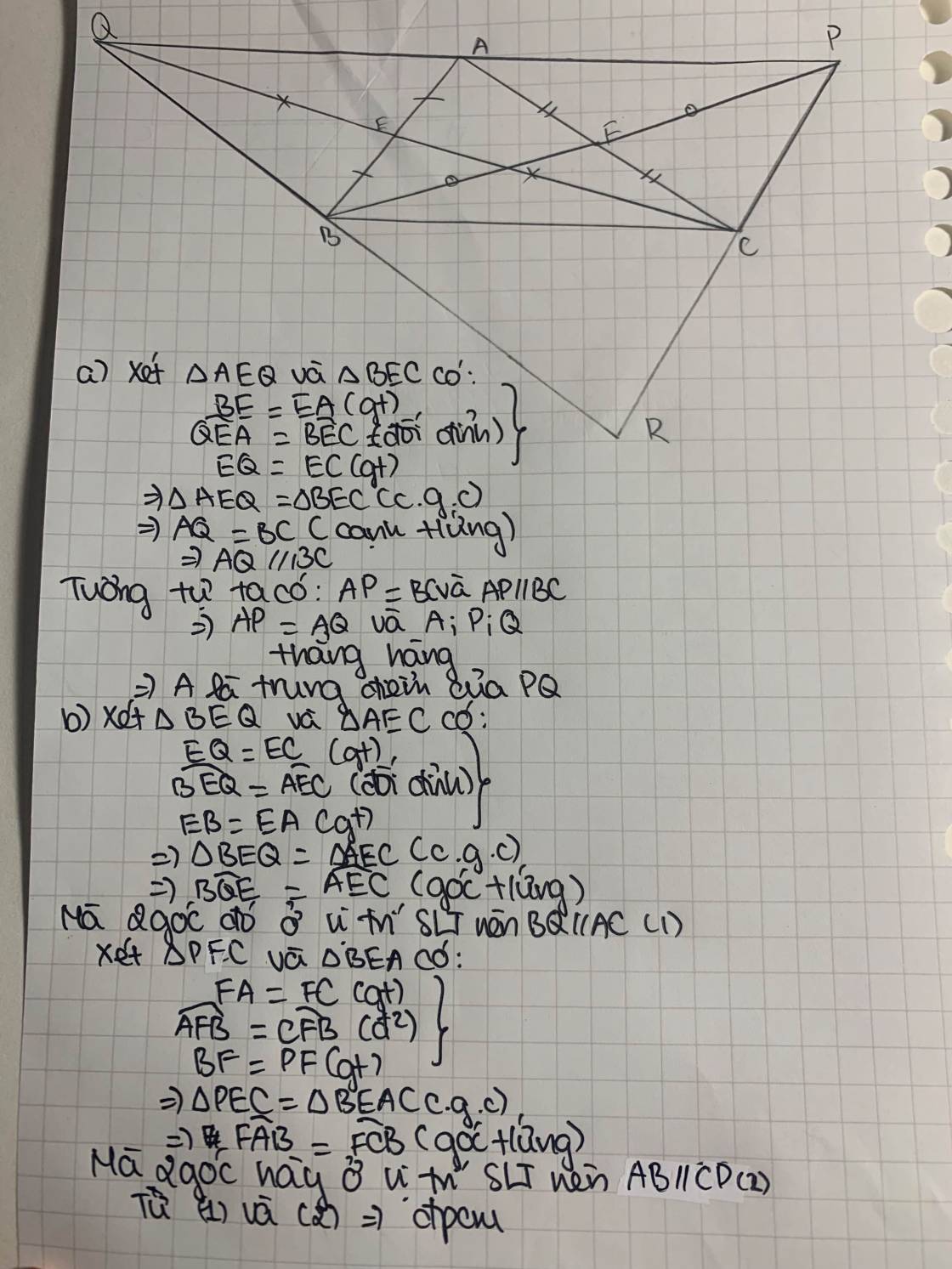
xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=>. tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ.
b) xét tam giác BEQ và tam giác AEC có
EQ=EC
BEQ=AEC đối đỉnh
EB=EA
=> tam giác BEQ = tam giác AEC(c.g.c)
=> BQE=AEC(góc tương ứng) mà chúng ở vị trí so le trong nên BQ//AC.
xét tam giác PFC và BFA có:
FA=FC
AFB=CFP
BF=PF
=. tam giác PFC = BFA (c.g.c)
=> FAB = FCB(góc tương ứng)
mà chúng ở vị trí so le trong nên
CP//AB
cho tớ 1 tick nhé! ^^ cảm ơn
vì Tam gáic AEQ = BEC nên QAE=CBE, mà chugns ở vị trí so le trong nên AQ//BC.
=> QAB=CBA
xét tam giác ABQ và tam giác ABC có
QAB=CAB
AB chung
CAB=QBA( AC//BQ)
vậy chúng bằng nhau(g.c.g)
AQB=ACB
mà AQB=CBR(đồng vị) từ hai điều này suy ra ACB=RBC
vì tam giác AFB=CFB nên A=C mà chúng ở vị trí so le trong nên AP//BC=>PAC=BCA
Xét tam giác ABC và PCA có
BAC=PCA(AB//PC)
AC chung
PAC=BCA(cmt)
vậy chúng bằng nhau theo truognừ hợp g.c.g
=>ABC=CPA
mà CPA=RCP( đồng vị) từ hai điều này suy ra ABC=RCB.
Xét tam giác ABC và RCB có
AQB=CBR
BC chung
CPA=RCP
vậy chúng bằng nhau theo truognừ hợp g.c.g
=> AB=RC;AC=RB(cạnh tuognư ứng)
* Vì AQ//BC,AP//BC, theo tiên đề Ơ-clit => ba điểm Q,A,P thẳng hàng
vì BC = AQ = AP nên BC = 1/2 QP
* Vì AC = BQ(cmt)
AC=BR(cmt)
nên AC = 1/2 QR
vì theo đề cho ba điểm Q,B,R đã thằng hàng nên không cần chứng minh. ba điểm P,C,R cũng vậy.
* Vì AB=CP(cmt)
AB=RC(cmt)
nên AB= 1/2 RP
ta có chu vi tam giác PQR = PQ + QR + RP = \(\frac{1}{2}BC+\frac{1}{2}AC+\frac{1}{2}AB=\frac{1}{2}\left(AB+AC+BC\right)=\frac{1}{2}\)chu vi ABC điều phải chứng minh.
d) Xét tam giác PQR có BQ=BR(cùng bằng AC)
CR=CP(cùng bằng AB)
AQ=AP(cmt) và Q,A,P thẳng hàng
suy ra B,C và A lần lượt là trung điểm của QR, RP và PQ.
gọi giao điểm của QC và BP là H
tam giác PQR có QC, PB và RA là các đuognừ trung tuyến giao nhau tại H nên H là trọng tâm. Xong
vậy 3 đường này đồng quy

a) xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=>. tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ.
b) xét tam giác BEQ và tam giác AEC có
EQ=EC
BEQ=AEC đối đỉnh
EB=EA
=> tam giác BEQ = tam giác AEC(c.g.c)
=> BQE=AEC(góc tương ứng) mà chúng ở vị trí so le trong nên BQ//AC.
xét tam giác PFC và BFA có:
FA=FC
AFB=CFP
BF=PF
=. tam giác PFC = BFA (c.g.c)
=> FAB = FCB(góc tương ứng)
mà chúng ở vị trí so le trong nên
CP//AB
Có thể loại đường trung bình nữa à Tuân Huỳnh Ngọc Minh???!!!