Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{3}{5}\)
nên \(\widehat{B}\simeq36^052'\)
Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-36^052'=53^08'\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot7,5=4,5\cdot6=27\)
=>AH=27/7,5=3,6(cm)

Ta có: ΔABC vuông tại B
nên \(\widehat{A}+\widehat{C}=90^0\)
hay \(\widehat{C}=23^0\)
Xét ΔABC vuông tại B có
\(AC=\dfrac{AB}{\cos67^0}\)
\(\Leftrightarrow AC\simeq20,47\left(cm\right)\)
\(\Leftrightarrow BC\simeq18,84\left(cm\right)\)

AC=căn 7^2-5^2=2căn6(cm)
sin C=5/7
=>góc C=45 độ 35'
=>góc B=44 độ 25'

\(AB=\cos B\cdot BC=\dfrac{1}{2}\cdot20=10\left(cm\right)\\ AC=\sin B\cdot BC=\dfrac{\sqrt{3}}{2}\cdot20=10\sqrt{3}\approx17,3205\left(cm\right)\\ \widehat{C}=90^0-\widehat{B}=30^0\)

Ta có \(\sin B=\sin48^0=\dfrac{AC}{BC}\approx0,74\Leftrightarrow BC\approx\dfrac{12}{0,74}\approx16,22\left(cm\right)\)
Áp dụng PTG: \(AB=\sqrt{BC^2-AC^2}\approx10,91\left(cm\right)\)
\(\widehat{C}=90^0-\widehat{B}=42^0\)

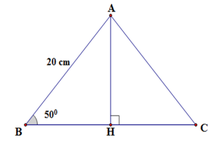
Kẻ AH ⊥ BC tại H. Suy ra H là trung điểm BC (do tam giác ABC cân tại A có AH vừa là đường cao vừa là đường trung tuyến)
Xét tam giác AHB vuông tại H có:
![]()
Mà H là trung điểm của BC nên:

Đáp án cần chọn là: B