Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

6.)
Khi 2 tam giác đồng dạng với nhau thì cạnh nhỏ nhất của tam giác này sẽ tương ứng với cạnh nhỏ nhất của tam giác kia.
Theo đề:\(A'B'\)=4,5
Ta có:\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(\Rightarrow\)\(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow\)\(B'C'=7,5cm,C'A'=10,5cm\)

Bài 7:
Đặt a=A'B',b=A'C', c=B'C'
Theo đề,ta có: a/6=b/8=c/10
mà cạnh nhỏ nhất trong tam giác A'B'C' là 9cm
nên b/8=c/10=9/6=3/2
=>b=12cm; c=15cm

Xét ΔABC có
D là trung điểm của AB
F là trung điểm của AC
Do đó: DF là đường trung bình của ΔABC
Suy ra: \(DF=\dfrac{BC}{2}\)
Xét ΔABC có
D là trung điểm của AB
E là trung điểm của BC
Do đó: DE là đường trung bình của ΔBAC
Suy ra: \(DE=\dfrac{AC}{2}\)
Xét ΔACB có
F là trung điểm của AC
E là trung điểm của BC
Do đó: FE là đường trung bình của ΔACB
Suy ra: \(FE=\dfrac{AB}{2}\)
Ta có: \(C_{DEF}=DF+DE+EF\)
\(=\dfrac{AB+AC+BC}{2}\)
\(=\dfrac{C_{ABC}}{2}\)

Chu vi tam giác ABC là 3 + 5 +7 = 15
Ta có :
P ABC / P A'B'C' = AB / A'B'
<=> 15 / 55 = 3 / A'B'
=> A'B' = ( 55 x 3 )/ 15 = 11 cm
P ABC / P A'B'C' = AC / A'C'
<=> 15 / 55 = 5 / A'C'
=> A'C' = ( 55 x 5 ) / 15 = 55/3 cm
P ABC / P A'B'C' = BC / B'C'
<=> 15 / 55 = 7 / B'C'
=> B'C' = ( 55 x 7 ) / 15 = 77/3 cm
\(\Rightarrow\Delta ABC\)đồng dạng \(\Delta A'B'C'\left(gt\right)\)
Áp dụng tính chất DTSBN , ta có :
\(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{AB+AC+BC}{A'B'+A'C'+B'C'}=\frac{C_{ABC}}{C_{A'B'C'}}\)
Hay \(\frac{3}{A'B'}=\frac{7}{B'C'}=\frac{5}{A'C'}=\frac{C_{ABC}}{55}=\frac{3+5+7}{55}=\frac{15}{55}=\frac{3}{11}\)
Với CABC và CA'B'C' lần lượt là chu vi của tam giác ABC , A'B'C'
\(+)\frac{3}{A'B'}=\frac{3}{11}\Rightarrow A'B'=\frac{3.11}{3}=11cm\)
\(+)\frac{7}{A'C'}=\frac{3}{11}\Rightarrow B'C'=\frac{7.11}{3}\approx25,67cm\)
\(+)\frac{5}{A'C'}=\frac{3}{11}\Rightarrow A'C'=\frac{5.11}{3}\approx18,33cm\)

a:
MC+MB=BC
=>BC=2MB+MB=3MB
=>\(\dfrac{CM}{CB}=\dfrac{2MB}{3MB}=\dfrac{2}{3}\)
Xét ΔCME và ΔCBA có
\(\widehat{CME}=\widehat{CBA}\)(hai góc đồng vị, ME//AB)
\(\widehat{C}\) chung
Do đó: ΔCME đồng dạng với ΔCBA
=>\(\dfrac{CM}{CB}=\dfrac{CE}{CA}=\dfrac{ME}{BA}=\dfrac{2}{3}\)
b: ΔCME đồng dạng với ΔCBA
=>\(\dfrac{C_{CME}}{C_{CBA}}=\dfrac{CM}{CB}=\dfrac{2}{3}\)
=>\(C_{CME}=\dfrac{2}{3}\cdot24=16\left(cm^2\right)\)

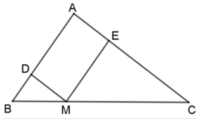
Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra :
D B A B = B M B C = D M A C = D B + B M + D M A B + B C + C A
Do đó 1 3 = P B D M P A B C
Chu vi ΔDBM bằng 30. 1 3 = 10cm
Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra
E M A B = M C B C = E C A C = E M + M C + E C A B + B C + A C
do đó 2 3 = P E M C P A B C
Chu vi ΔEMC bằng 30. 2 3 = 20 cm
Vậy chu vi ΔDBM và chu vi ΔEMC lần lượt là 10cm; 20cm
Đáp án: D
Gọi độ dài cạnh BC là a (cm) ( a>0)
Vì \(BC=2AB\Rightarrow AB=\frac{BC}{2}=\frac{a}{2}\)
Vì \(BC=\frac{4}{5}AC\Rightarrow AC=BC:\frac{4}{5}=BC.\frac{5}{4}=\frac{5a}{4}\)
Vì chu vi của tam giác ABC =30cm
\(\Rightarrow a+\frac{a}{2}+\frac{5a}{4}=30\)
\(\Leftrightarrow\frac{11}{4}a=30\)
\(\Leftrightarrow a=\frac{120}{11}\Rightarrow BC=\frac{120}{11}cm\)
\(\Rightarrow AB=\frac{60}{11}cm\)
\(\Rightarrow AC=\frac{150}{11}cm\)