Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(BM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right)\)
Tam giác ABM có MD là p/giác
\(\Rightarrow\dfrac{AD}{BD}=\dfrac{AM}{BM}=\dfrac{6}{5}\)
b) Tam giác AMC có ME là p/giác
\(\Rightarrow\dfrac{MC}{AM}=\dfrac{EC}{AE}\)
Mà: MC = BM (GT)
\(\Rightarrow\dfrac{BM}{AM}=\dfrac{EC}{AE}\)
c) Có: \(\dfrac{AD}{BD}=\dfrac{AM}{BM}\left(cmt\right)\) (1)
Tam giác AMC có ME là p/giác
\(\Rightarrow\dfrac{AE}{EC}=\dfrac{AM}{MC}\)
Mà: BM = MC (GT)
\(\Rightarrow\dfrac{AE}{EC}=\dfrac{AM}{BM}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{EC}\)
=> DE // BC
a) Ta có: M là trung điểm của BC(gt)
nên \(MB=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Xét ΔAMB có MD là đường phân giác ứng với cạnh AB(Gt)
nên \(\dfrac{AD}{BD}=\dfrac{AM}{BM}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{AD}{BD}=\dfrac{6}{5}\)

Do M là trung điểm của BC nên:
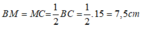
Theo tính chất tia phân giác của góc ta có:
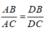
Suy ra:
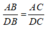
Theo tính chất của dãy tỉ số bằng nhau ta có:
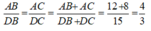
Suy ra:
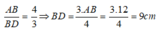
Do đó:
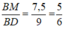
Chọn đáp án A

Do M là trung điểm của BC nên:
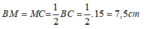
Theo tính chất tia phân giác của góc ta có:
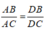
Suy ra:
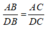
Theo tính chất của dãy tỉ số bằng nhau ta có:
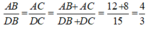
Suy ra:
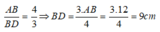
Do đó:
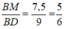
Chọn đáp án A

a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm

Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{6}=\dfrac{4}{8}=\dfrac{1}{2}\)
=>\(BD=\dfrac{6}{2}=3\left(cm\right)\)

1: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc ACB chung
Do đó: ΔABC\(\sim\)ΔHAC
2: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Xét ΔABC có AM là phân giác
nên BM/AB=CM/AC
=>BM/3=CM/4
Áp dụng tính chất của dãy tr số bằng nhau, ta được:
\(\dfrac{BM}{3}=\dfrac{CM}{4}=\dfrac{BM+CM}{3+4}=\dfrac{25}{7}\)
Do đó: BM=75/7(cm); CM=100/7(cm)