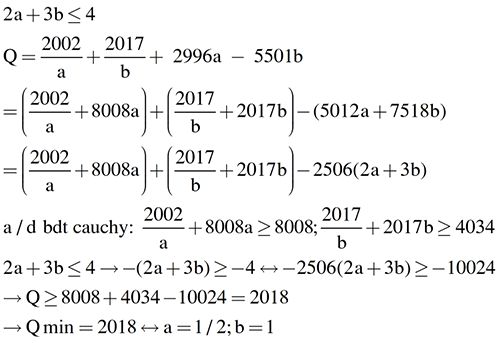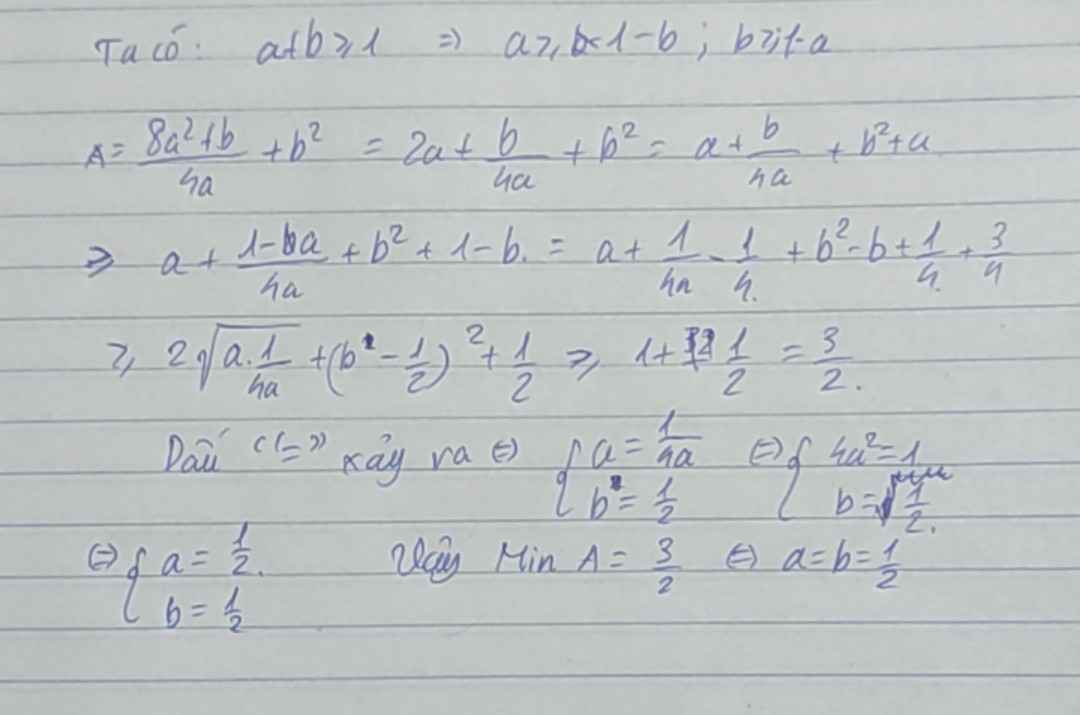Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ \(2a+b+c=\left(a+b\right)+\left(a+c\right)\)
\(\ge2\sqrt{\left(a+b\right)\left(a+c\right)}\) ( theo AM-GM )
\(\Rightarrow\left(2a+b+c\right)^2\ge4\left(a+b\right)\left(a+c\right)\)
\(\Rightarrow\frac{1}{\left(2a+b+c\right)^2}\le\frac{1}{4\left(a+b\right)\left(a+c\right)}\)
Dấu "=" xảy ra \(\Leftrightarrow b=c\)
+ Tương tự : \(\frac{1}{\left(2b+c+a\right)^2}\le\frac{1}{4\left(a+b\right)\left(b+c\right)}\). Dấu "=" xảy ra <=> a = c
\(\frac{1}{\left(2c+a+b\right)^2}\le\frac{1}{4\left(a+c\right)\left(b+c\right)}\). Dấu "=" xảy ra \(\Leftrightarrow a=b\)
Do đó : \(P\le\frac{1}{4}\left(\frac{1}{\left(a+b\right)\left(a+c\right)}+\frac{1}{\left(a+b\right)\left(b+c\right)}+\frac{1}{\left(a+c\right)\left(b+c\right)}\right)\)
\(\Rightarrow P\le\frac{1}{2}\cdot\frac{a+b+c}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
\(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}\cdot2\sqrt{bc}\cdot2\sqrt{ca}\)\(=8abc\)
\(\Rightarrow P\le\frac{a+b+c}{16abc}\)
+ \(\frac{1}{a^2}+\frac{1}{b^2}\ge\frac{2}{ab}\). Dấu :=" xảy ra \(\Leftrightarrow a=b\)
\(\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{2}{bc}\). Dấu "=" xảy ra <=> b = c
\(\frac{1}{c^2}+\frac{1}{a^2}\ge\frac{2}{ca}\). Dấu "=" xảy ra <=> c = a
\(\Rightarrow2\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\ge2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)\)
\(\Rightarrow3\ge\frac{a+b+c}{abc}\) \(\Rightarrow a+b+c\le3abc\)
\(\Rightarrow P\le\frac{3abc}{16abc}=\frac{3}{16}\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c=1\)

* Vì \(a,b\ge1\)nên \(\left(a-1\right)\left(b-1\right)\ge0\Leftrightarrow ab+1\ge a+b\)
Một cách tương tự: \(bc+1\ge b+c;ca+1\ge c+a\)
Với mọi số thực \(a\ge1\) ta luôn có: \(\left(a-1\right)^2\ge0\Leftrightarrow a^2\ge2a-1\Leftrightarrow\frac{1}{2a-1}\ge\frac{1}{a^2}\)
Tương tự: \(\frac{1}{2b-1}\ge\frac{1}{b^2};\frac{1}{2c-1}\ge\frac{1}{c^2}\)
Từ đó suy ra \(VT\ge\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{4ab}{ab+1}+\frac{4bc}{bc+1}+\frac{4ca}{ca+1}\)\(=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+4-\frac{4}{ab+1}+4-\frac{4}{bc+1}+4-\frac{4}{ca+1}\)\(\ge\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}-\frac{4}{ab+1}-\frac{4}{bc+1}-\frac{4}{ca+1}+12\)\(\ge\frac{4}{\left(a+b\right)^2}+\frac{4}{\left(b+c\right)^2}+\frac{4}{\left(c+a\right)^2}-\frac{4}{a+b}-\frac{4}{b+c}-\frac{4}{c+a}+12\)\(=\left(\frac{2}{a+b}-1\right)^2+\left(\frac{2}{b+c}-1\right)^2+\left(\frac{2}{c+a}-1\right)^2+9\ge9\)
Đẳng thức xảy ra khi a = b = c = 1

Lời giải:
\(a+b+c+ab+bc+ac+abc=0\)
\(\Leftrightarrow (a+b+ab+1)+c+bc+ac+abc=1\)
\(\Leftrightarrow (a+b+ab+1)+c(1+b+a+ab)=1\)
\(\Leftrightarrow (a+1)(b+1)+c(a+1)(b+1)=1\)
\(\Leftrightarrow (a+1)(b+1)(c+1)=1\)
Đặt \((a+1,b+1,c+1)=(x,y,z)\Rightarrow (a,b,c)=(x-1,y-1,z-1)\) và \(xyz=1\)
Khi đó:
\(P=\frac{1}{3+2(x-1)+y-1+(x-1)(y-1)}+\frac{1}{3+2(y-1)+z-1+(y-1)(z-1)}+\frac{1}{3+2(z-1)+x-1+(x-1)(z-1)}\)
\(=\frac{1}{x+xy+1}+\frac{1}{y+yz+1}+\frac{1}{z+xz+1}\)
\(=\frac{yz}{xyz+xy.yz+yz}+\frac{1}{y+yz+1}+\frac{y}{zy+xz.y+y}\)
\(=\frac{yz}{1+y+yz}+\frac{1}{y+yz+1}+\frac{y}{yz+1+y}=\frac{yz+1+y}{yz+1+y}=1\)
Ta có đpcm.

Lời giải:
Áp dụng BĐT AM-GM ta có:
\(2a+b+c=(a+b)+(a+c)\geq 2\sqrt{(a+b)(a+c)}\)
\(\Rightarrow (2a+b+c)^2\geq 4(a+b)(a+c)\)
\(\Rightarrow \frac{1}{(2a+b+c)^2}\leq \frac{1}{4(a+b)(a+c)}\)
Hoàn toàn tương tự với các phân thức còn lại suy ra:
\(P\leq \frac{1}{4}\left(\frac{1}{(a+b)(a+c)}+\frac{1}{(b+c)(b+a)}+\frac{1}{(c+a)(c+b)}\right)\)
\(\Leftrightarrow P\leq \frac{1}{4}.\frac{(b+c)+(c+a)+(a+b)}{(a+b)(b+c)(c+a)}\)
\(\Leftrightarrow P\leq \frac{a+b+c}{2(a+b)(b+c)(c+a)}\)
Lại có: \((a+b)(b+c)(c+a)\geq 2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ac}=8abc\) (theo AM-GM)
\(\Rightarrow P\leq \frac{a+b+c}{2.8abc}=\frac{a+b+c}{16abc}(1)\)
Tiếp tục áp dụng BĐT AM-GM:
\(\frac{1}{a^2}+\frac{1}{b^2}\geq \frac{2}{ab}; \frac{1}{b^2}+\frac{1}{c^2}\geq \frac{2}{bc}; \frac{1}{c^2}+\frac{1}{a^2}\geq \frac{2}{ac}\)
\(\Rightarrow 2\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\geq 2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)\)
\(\Leftrightarrow 3\geq \frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}=\frac{a+b+c}{abc}\)
\(\Rightarrow a+b+c\leq 3abc(2)\)
Từ \((1); (2)\Rightarrow P\leq \frac{3abc}{16abc}=\frac{3}{16}\)
Vậy \(P_{\max}=\frac{3}{16}\). Dấu bằng xảy ra khi \(a=b=c=1\)

Ta có:
\(Q=\dfrac{2002}{a}+\dfrac{2017}{b}+2996a-5501b\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-\left(5012a+7518b\right)\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-2506\left(2a+3b\right)\)
Áp dụng BĐT Cauchy cho hai số không âm ta có:
\(\dfrac{2002}{a}+8008a\ge2\sqrt{\dfrac{2002}{a}.8008a}=2.4004=8008\) (1)
\(\dfrac{2017}{b}+2017b\ge2\sqrt{\dfrac{2017}{b}.2017b}=2.2017=4034\) (2)
Có \(2a+3b\le4\Rightarrow-\left(2a+3b\right)\ge-4\Rightarrow-2506\left(2a+3b\right)\ge-10024\)(3)
Từ (1), (2) và (3) \(\Rightarrow Q\ge8008+4034-10024=2018\)
Dấu '=' xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2002}{a}=8008a\\\dfrac{2017}{b}=2017b\\2a+3b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)
Vậy,...
![]()