K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ST
1
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2021
Thay tọa độ A và B vào pt \(\Delta\) được 2 giá trị trái dấu \(\Rightarrow A;B\) nằm khác phía so với \(\Delta\)
\(\Rightarrow MA+MB\) nhỏ nhất khi và chỉ khi M nằm trên giao điểm của đường thẳng AB và \(\Delta\)
\(\overrightarrow{AB}=\left(1;2\right)\Rightarrow\) đường thẳng AB nhận (2;-1) là 1 vtpt
Phương trình AB: \(2\left(x+1\right)-1\left(y-1\right)=0\Leftrightarrow2x-y+3=0\)
Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}2x-y+3=0\\x+y-2=0\end{matrix}\right.\) \(\Rightarrow M\left(-\dfrac{1}{3};\dfrac{7}{3}\right)\)
CM
13 tháng 8 2018
Đáp án D
Do M thuộc d nên M( x; 2x+ 3)
Suy ra:
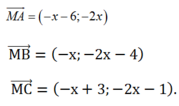
Do đó:
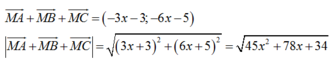
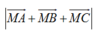
nhỏ nhất khi và chỉ khi: f(x) = 45x2+ 78x + 34 nhỏ nhất
11 tháng 12 2021
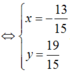
a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |
DD
0
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 6 2020
Gọi \(A\left(a;1-a\right)\) ; \(B\left(b;2b-1\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(a-1;2-a\right)\\\overrightarrow{MB}=\left(b-1;2b\right)\end{matrix}\right.\)
\(2\overrightarrow{MA}+\overrightarrow{MB}=0\Leftrightarrow\left(2a-2;4-2a\right)+\left(b-1;2b\right)=\left(0;0\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a-2+b-1=0\\4-2a+2b=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2a+b=3\\-2a+2b=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{5}{3}\\b=-\frac{1}{3}\end{matrix}\right.\)
\(\Rightarrow A\left(\frac{5}{3};-\frac{2}{3}\right);B\left(-\frac{1}{3};-\frac{5}{3}\right)\) \(\Rightarrow\overrightarrow{AB}=\left(2;1\right)\)
Phương trình AB:
\(1\left(x-\frac{5}{3}\right)-2\left(y+\frac{2}{3}\right)=0\Leftrightarrow x-2y-3=0\)
CT
0