Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Ta có:
\(\dfrac{a}{b}=\dfrac{-8}{11}\left(1\right)\Leftrightarrow1-\dfrac{a}{b}=1-\dfrac{-8}{11}\)
Hay \(\dfrac{b-a}{b}=\dfrac{11+8}{11}=\dfrac{19}{11}\left(2\right)\)
Thay \(b-a=190\) vào \(\left(2\right)\) ta được:
\(\dfrac{190}{b}=\dfrac{19}{11}\Leftrightarrow190.11=19b\Leftrightarrow b=110\)
Thay \(b=110\) vào \(\left(1\right)\) ta được:
\(\dfrac{a}{110}=\dfrac{-8}{11}\Leftrightarrow11a=-8.110\Leftrightarrow a=-80\)
Vậy phân số \(\dfrac{a}{b}\) cần tìm là \(\dfrac{-80}{110}\)
Thay b - a = 190 vào (1) ta được:
Phân số a/b phải tìm là -80/110

Ta có a/b=3/4
Nếu thêm 15 đơn vị vào tử và giữ nguyên mẫu số rồi rút gọn thì ta được phân số 7/6
==>a* 15/6=7/6
==>a/b+15/6=7/6
==>15/6=7/6 -3/4=5/12
==> 180=5b
==>b=180*5=36

Vì nếu rút gọn \(\frac{a}{b}\)thì được phân số \(\frac{9}{13}\)=> \(\frac{a}{b}=\frac{9k}{13k}\left(k\in Z;k\ne0\right)\)
Ta có: \(\frac{9k}{13k-35}=\frac{27}{32}\)
=> \(9.k.32=27.\left(13.k-35\right)\)
=> \(288.k=351.k-945\)
=> \(351.k-288.k=945\)
=> \(63.k=945\)
=> \(k=945:63=15\)
=> \(\frac{a}{b}=\frac{9.15}{13.15}=\frac{135}{195}\)

a. \(\dfrac{-3}{5}\)
b. \(\dfrac{-2}{3}\) c. \(\dfrac{4}{39}\) d. \(\dfrac{26}{45}\)

Vì cộng cả tử và mẫu của phân số \(\dfrac{23}{40}\) với cùng một số tự nhiên n rồi rút gọn ta được \(\dfrac{3}{4}\) nên ta được:
\(\dfrac{23+n}{40+n}=\dfrac{3}{4}\)
\(\Rightarrow\)\(4.\left(23+n\right)=3.\left(40+n\right)\)
hay 92 + 4.n = 120 + 3.n
4.n - 3.n = 120 - 92
\(\Rightarrow\) n = 28
Vậy số tự nhiên n cần tìm là 28
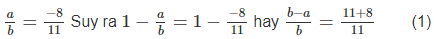
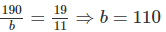
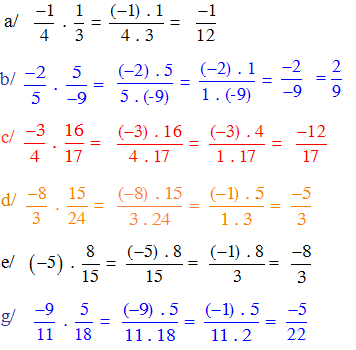

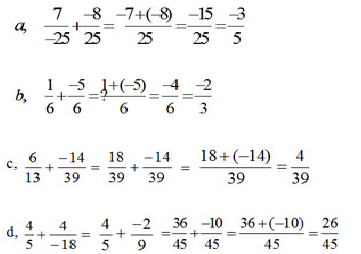
Ta có: \(\dfrac{9}{11}=\dfrac{36}{44};\dfrac{5}{4}=\dfrac{55}{44}\)
Khi đó giá trị 1 phần là: \(38:\left(55-36\right)=2\)
\(\Rightarrow\) Tử số: \(36.2=72\)
Mẫu: \(44.2=88\)
Vậy \(\dfrac{a}{b}=\dfrac{72}{88}.\)