Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 5x + 10 = 5(x + 2)
25x2 + 50x = 25x(x + 2)
⇒ Nhân tử chung của chúng là: 5(x + 2)
b)
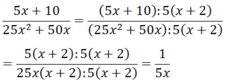

Ta có: \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{2{\rm{x}}}}{{x + 1}}\)

Chia cả tử và mẫu của phân thức này cho nhân tử chung x−1, ta có \(\frac{{x + 1}}{{{x^2} + x + 1}}\)
=> Phân thức mới được rút gọn và mất đi nhân tử chung x−1

Ta có phân thức mới là
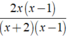
Ta có
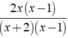
= (2x)/(x + 2)
vì 2x( x - 1 ).( x + 2 ) = 2x.( x + 2 )( x - 1 ).

Ta có: \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
Nhân tử chung là x + 1

x.(x + 2) = x2 + 2x
3.(x +2) = 3x + 6
⇒ x(3x + 6) = 3(x2 + 2x) = 3x2 + 6x
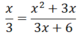
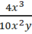
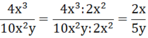
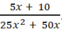
a) Ta có: \(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}} = \dfrac{{2{\rm{x}}.2{\rm{x}}y}}{{3y.2{\rm{x}}y}}\)
Nhân tử chung của cả tử và mẫu là: 2xy
b) Chia cả tử và mẫu của phân thức đã cho cho nhân tử chung 2xy ta được:
\(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}} = \dfrac{{\left( {4{{\rm{x}}^2}y} \right):2{\rm{x}}y}}{{\left( {6{\rm{x}}{y^2}} \right):2{\rm{x}}y}} = \dfrac{{2{\rm{x}}}}{{3y}}\)