TT
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VM
0
10 tháng 3 2020
a) Ta có: \(a=\left[n\left(n+3\right)\right]\left[\left(n+1\right)\left(n+2\right)\right]+1\)
\(=\left(n^2+3n\right)\left(n^2+3n+2\right)+1\)
Đặt \(n^2+3n+1=t\)(1)
Khi đó: \(a=\left(t-1\right)\left(t+1\right)+1=t^2-1+1=t^2\)
\(\Rightarrow\) a là số chính phương
b) Để a=121 thì \(t^2=121\)\(\Rightarrow t=\pm11\)
+ Với t=11 thì (1) \(\Leftrightarrow n^2+3n+1=11\Leftrightarrow n^2+3n-10=0\)
\(\Leftrightarrow\left(n-2\right)\left(n+5\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}n=2\\n=-5\end{cases}}\)
+ Với n=-11 thì (1)\(\Leftrightarrow n^2+3n+1=-11\Leftrightarrow n^2+3n+12=0\)
\(\Leftrightarrow\left(n-\frac{3}{2}\right)^2+\frac{39}{4}=0\) ( vô lý)
Do đó, pt vo nghiệm
Vậy để a=121 thì n =2 hoặc n=-5
LK
3
HT
0
25 tháng 11 2023
a: Để (1) là hàm số bậc nhất thì \(\sqrt{m-1}< >0\)
=>m-1>0
=>m>1
b: Để (1) trùng với đường thẳng y=2x-1 thì \(\left\{{}\begin{matrix}\sqrt{m-1}=2\\2n-3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-1=4\\2n=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=5\\n=1\end{matrix}\right.\)
20 tháng 2 2016
Vì đa thức (x−a)(x−10)+1(x−a)(x−10)+1 có thể phân tích thành tích của hai đa thức bậc nhất có hệ số nguyên nên ta chỉ có hai cách phân tích duy nhất là:
1)(x−a)(x−10)=(x+b)(x+c)2)(x−a)(x−10)=(−x+b)(−x+c)1)(x−a)(x−10)=(x+b)(x+c)2)(x−a)(x−10)=(−x+b)(−x+c) với b,c∈Zb,c∈Z
Ta sẽ tìm aa trong trường hợp 1)1), trường hợp còn lại làm tương tự
(x−a)(x−10)+1=(x−b)(x−c)⇔x2−(a+10)x+10a+1=x2+(b+c)x+bc(x−a)(x−10)+1=(x−b)(x−c)⇔x2−(a+10)x+10a+1=x2+(b+c)x+bc
Đồng nhất, ta được {b+c=−(a+10)bc=10a+1{b+c=−(a+10)bc=10a+1
⇒b,c⇒b,c là hai nghiệm nguyên của PT X2+(a+10)X+10a+1=0X2+(a+10)X+10a+1=0 với aa nguyên
⇒Δ=(a+10)2−40a−4=m2(m∈N)⇔(a−10)2−4=m2⇔(a−m−10)(a+m−10)=4⇒Δ=(a+10)2−40a−4=m2(m∈N)⇔(a−10)2−4=m2⇔(a−m−10)(a+m−10)=4
Vì a−m−10a−m−10 và a+m−10a+m−10 cùng tính chẵn lẻ và a+m−10≥a−m−10a+m−10≥a−m−10 nên:
{a+m−10=2a−m−10=2⇒a=12{a+m−10=2a−m−10=2⇒a=12
Hoặc :
{a+m−10=−2a−m−10=−2⇒a=8
20 tháng 2 2016
\(x^2-\left(a+10\right)x+10a+1=0\)
\(\Delta=a^2+20a+100-40a-4=\left(a-10\right)^2-4=\left(a-6\right)\left(a-14\right)\)
a thuộc Z => \(\Delta\) là số nguyên ; để TM yêu cầu => \(\Delta\) là số chính phương
=> a =6 ; a =14
9 tháng 4 2018
a)
(pt1) ; 2k +1 =5 => k =2
(pt2): 2 -1 = vậy k =2 nhận
b)
hệ có nghiệm duy nhất; <=> k khác -1
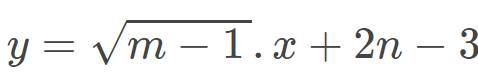
A nguyên <=> 13 chia hết cho n-1
Hay n-1 là ước của 13= (1;13)
Hay n= 2 hoặc n=14
=>13 chia hết cho n-1
=>n-1 là ước của 13
sau đó bn liệt kê các ước của 13 ra rồi thay n-1 vầy rồi tìm giá trị
k mik nha