Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm của (P) và d: x 2 − m x + 2 = 0 (1)
P) cắt d tại hai điểm phân biệt A(x1;y1) và B(x2;y2) ⇔ (1) có hai nghiệm phân biệt
⇔ ∆ = m2 – 4.2 > 0 ⇔ m2 > 8 ⇔ m > 2 2 hoặc m<- 2 2
Khi đó x1, x2 là nghiệm của (1). Áp dụng định lí Vi–ét ta có x1 + x2 = m; x1x2 = 2.
Do A, B ∈ d nên y1 = mx1 – 2 và y2 = mx2 – 2.
Ta có:
y 1 + y 2 = 2 ( x 1 + x 1 ) − 1 < = > m x 1 − 2 + m x 2 − 2 = 2 ( x 1 + x 2 ) − 1 < = > ( m − 2 ) ( x 1 + x 2 ) − 3 = 0 < = > m ( m − 2 ) − 3 = 0 < = > m 2 − 2 m − 3 = 0
⇔ m = –1 (loại) hoặc m = 3 (thỏa mãn)
Vậy m = 3 là giá trị cần tìm.

Trả lời:
Phương trình hoành độ giao điểm (P) và (d) ta có:
\(-x^2=2x+m-1\)
\(\Leftrightarrow x^2+2x+m-1=0\)(1)
Ta có: \(\Delta=2^2-4.1.\left(m-1\right)\)
\(=4-4m+4\)
\(=8-4m\)
Để phương trình (1) có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow8-4m>0\)
\(\Leftrightarrow4m< 8\)
\(\Leftrightarrow m< 2\)
\(\Rightarrow\)Phương trình (1) có 2 nghiệm phân biệt
\(\Rightarrow\)(d) cắt (P) tại 2 diểm phân biệt \(A\left(x_1,y_1\right);B\left(x_2,y_2\right)\)
Áp dụng Vi-ét \(\hept{\begin{cases}x_1+x_2=-2\left(1\right)\\x_1.x_2=m-1\left(2\right)\end{cases}}\)
Ta có \(y_1=-x_1^2\); \(y_2=-x_2^2\)
Theo đề bài:
\(x_1.y_1-x_2.y_2-x_1.x_2=4\)
\(\Leftrightarrow x_1.\left(-x_1^2\right)-x_2.\left(-x_2^2\right)-x_1.x_2=4\)
\(\Leftrightarrow-x_1^3+x_2^3-x_1.x_2=4\)
\(\Leftrightarrow-\left(x_1^3-x_2^3\right)-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(x_1^2+x_1.x_2+x_2^2\right)-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right)\left[\left(x_1+x_2\right)^2-2x_1.x_2+x_1.x_2\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left[\left(x_1+x_2\right)^2-x_1.x_2\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left[\left(-2\right)^2-m+1\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(4-m+1\right)=4+m-1\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(3-m\right)=m+3\)
\(\Leftrightarrow-\left(x_1-x_2\right)=\frac{m+3}{3-m}\)
\(\Leftrightarrow x_1-x_2=\frac{m+3}{m-3}\)(3)
Từ (1) (3) ta có: \(\hept{\begin{cases}x_1+x_2=-2\\x_1-x_2=\frac{m+3}{m-3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x_1=-2+\frac{m+3}{m-3}=\frac{9-m}{m-3}=-\left(m+3\right)\\x_1+x_2=-2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1=\frac{-\left(m+3\right)}{2}\\x_2=\frac{m-1}{2}\end{cases}}\)
Thay x1, x2 vào (2) ta có
\(x_1.x_2=m-1\)
\(\Leftrightarrow\frac{-\left(m+3\right)}{2}.\frac{m-1}{2}=m-1\)
\(\Leftrightarrow\frac{-\left(m+3\right)}{2}=2\)
\(\Leftrightarrow-\left(m+3\right)=4\)
\(\Leftrightarrow m+3=-4\)
\(\Leftrightarrow m=-7\)(TM)
Vậy \(m=-7\) thì thỏa mãn bài toán

PTHĐGĐ là:
x^2-(2m+1)x+2m=0
Δ=(2m+1)^2-4*2m
=4m^2+4m+1-8m=(2m-1)^2
Để (P) cắt (d) tại hai điểm phân biệt thì 2m-1<>0
=>m<>1/2
y1+y2-x1x2=1
=>(x1+x2)^2-3x1x2=1
=>(2m+1)^2-3*2m=1
=>4m^2+4m+1-6m-1=0
=>4m^2-2m=0
=>m=0 hoặc m=1/2(loại)

đường thẳng \(d^'\)và \(d\)cắt nhau tại một điểm A trên trục tung nên điểm A có hoành độ \(x_a=0\)và tạo độ A thỏa mãn phương trình \(d^'\)nên :\(\Rightarrow y_a=-2.0+1=1\)\(\Rightarrow A\left(0;1\right)\)Mà do a là giao điểm của 2 đường \(d;d^'\)nên toạn độ A cũng thỏa mãn phương trình của \(d\): \(\Rightarrow1=-m^2+m+1\Leftrightarrow m^2-m=0\Leftrightarrow m\left(m-1\right)=0\Leftrightarrow m\orbr{\begin{cases}m=0\\m=1\end{cases}}\)
câu b :
Xét phương trình hoành độ gia điểm của P và d có :
\(x^2=2mx-m^2+m+1\Leftrightarrow x^2-2mx+m^2-m-1=0\)
để hai đồ thị cắt nhau tại 2 điểm phân biệt thì \(\Delta^'=m^2+m^2-m-1=2m^2-m-1>0\)
\(\left(m-1\right)\left(2m+1\right)>0\Leftrightarrow\orbr{\begin{cases}m< -\frac{1}{2}\\m>1\end{cases}}@\)
khi đó theo vieet có :\(\hept{\begin{cases}x_1+x_2=2m\\x_1x_2=-m^2+m+1\end{cases}}\)
\(\Rightarrow y_1+y_2+2\left(x_1+x_2\right)=22\)với \(y_1=x^2_1;y_2=x_2^2\)
\(\Rightarrow\left(\left(x_1+x_2\right)^2-2x_1.x_2\right)+\left(x_1+x_2\right)2=22\)thay vieet ta có :
\(\left(2m\right)^2-2\left(-m^2+m+1\right)+2.2m=22\)
\(\Leftrightarrow6m^2+2m-24=0\Leftrightarrow\orbr{\begin{cases}m=\frac{-1+\sqrt{144}}{6}\\m=\frac{-1-\sqrt{144}}{6}\end{cases}}\)thỏa mãn @
Kết luận nghiệm
tính denta sai rùi rùi bạn ơi
phải là 145 chứ ko phải 144

Xét pt hoành độ gđ của (d) và (P) có:
\(x^2=2x+4m^2-8m+3\)
\(\Leftrightarrow x^2-2x-4m^2+8m-3=0\) (1)
\(\Delta=4-4\left(-4m^2+8m-3\right)\)\(=16m^2-32m+16=16\left(m-1\right)^2\)
Để (P) và (d) cắt nhau tại hai điểm pb khi pt (1) có hai nghiệm phân biệt \(\Leftrightarrow\Delta>0\Leftrightarrow m\ne1\)
Có \(A\in\left(P\right)\Rightarrow y_1=x_1^2\)
\(B\in\left(P\right)\Rightarrow y_2=x_2^2\) , trong đó x1; x2 là hai nghiệm của pt (1)
Theo định lí viet có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-4m^2+8m-3\end{matrix}\right.\)
\(y_1+y_2=10\)
\(\Leftrightarrow x_1^2+x_2^2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(-4m^2+8m-3\right)=10\)
\(\Leftrightarrow8m^2-16m=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)(tm)
Vậy...

Khi m =3
=> hàm số trở thành y=2x-3+3=2x
Hoành độ giao điểm (p) và (d) là nghiệm pt
\(x^2=2x\)
<=> x2-2x=0
<=> x(x-2)=0
<=> x=0 hoặc x=2
với x=0 thay vào (P) ta có y=02=0
với x=2thay vào (P) ta có y=22=4
Vậy (P) và (d) cắt nhau tại 2 điểm có tọa độ (0;0)và (2;4) khi m =3
b) Hoành độ giao điểm (p) và (d) là nghiệm pt
\(x^2=2x-m+3\)
\(x^2-2x+m-3=0\)
ta có \(\Delta\)=\(2^2-4\left(m-3\right)\)=\(4-4m+12\)
=\(16-4m\)
Để (p) và (d ) cắt nhau tại 2 điểm phân biệt thì 16-4m>0 hay m<4
Theo Vi ét ta có x1+x2=2
x1.x2=m-3
Và y1=x12; y2=x22
Khi đó x1.x2.( y1+y2)=-6
<=> (m-3) . ( x12+x22)=-6
<=> (m-3). ((x1+x2)2-2x1x2)=-6
<=> (m-3). (4-2m+6)=-6
Tự lm nốt nha bn ! ( mk mỏi tay quá :) ) ( nhớ k mk đấy )

PTHĐGĐ là;
x^2-3x-m^2+1=0
Δ=(-3)^2-4(-m^2+1)=4m^2-4+9=4m^2+5>0
=>Phương trình luôn có hai nghiệm phân biệt
TH1: x1>0; x2>0
=>x1+2x2=3
mà x1+x2=3
nên x1=1; x2=1
x1*x2=-m^2+1
=>-m^2+1=1
=>m=0
TH2: x1<0; x2>0
=>-x1+2x2=3 và x1+x2=3
=>x1=1; x2=2
x1*x2=-m^2+1
=>-m^2+1=2
=>-m^2-1=0(loại)
TH2: x1>0; x2<0
=>x1-2x2=0 va x1+x2=3
=>x1=2 và x2=1
x1*x2=-m^2+1
=>-m^2+1=2
=>-m^2=1(loại)
TH3: x1<0; x2<0
=>-x1-2x2=3 và x1+x2=3
=>x1=9 và x2=-6
x1*x2=-m^2+1
=>-m^2+1=-54
=>-m^2=-55
=>\(m=\pm\sqrt{55}\)
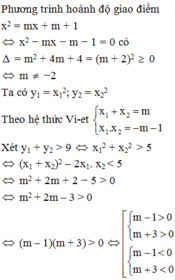
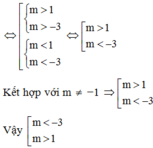
xét pt hoành độ giao điểm của đg thẳng (P) và (d) ta có:
\(-x^2=2x+m-1\)
\(x^2+2x+m-1=0\)
Aps dụng viet:
x1+x2=-2
x1.x2=m-1
vì (x1;y1) thuộc (P)=>y1=x1^2
ta có:x1y1-x2y2-x1x2=-4
<=>\(x_1x_1^2-x_2x_2^2-x1x2=-4\)
mk chỉ làm tới đây thôi còn lại bạn tự làm nốt nhá(mk lười):)))