Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Pt hoành độ giao điểm: \(x^2+mx+1=0\)
\(\Delta=m^2-4>0\) \(\Rightarrow\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\) ; khi đó \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=1\end{matrix}\right.\)
\(A=\dfrac{\left(x_1-x_2\right)^2}{x_1+x_2+1}=\dfrac{\left(x_1+x_2\right)^2-4x_1x_2}{x_1+x_2+1}=\dfrac{m^2-4}{-m+1}\)
\(A=-m-1+\dfrac{3}{m-1}\)
Để A nguyên \(\Rightarrow\dfrac{3}{m-1}\) nguyên \(\Rightarrow m-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Mà \(\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m-1>1\\m-1< -3\end{matrix}\right.\)
\(\Rightarrow m-1=3\Rightarrow m=4\)
b/ Gọi \(M\left(a;b\right)\) với \(\left\{{}\begin{matrix}-1\le a\le3\\b=a^2\end{matrix}\right.\) và \(C\left(3;1\right)\)
\(\Rightarrow S_{MAB}=S_{ABC}-\left(S_{BCM}+S_{ACM}\right)\) \(\Rightarrow S_{MAB}\) lớn nhất khi và chỉ khi\(S_{BCM}+S_{ACM}\) nhỏ nhất
Ta có \(S_{BCM}+S_{ACM}=\left(x_C-x_B\right)\left(y_M-y_B\right)+\left(y_A-y_C\right)\left(x_A-x_M\right)\)
\(=4\left(b-1\right)+8\left(3-a\right)=4a^2-4+24-8a\)
\(=4\left(a^2-2a+1\right)+16=4\left(a-1\right)^2+16\ge16\)
\(\Rightarrow\left(S_{BCM}+S_{ACM}\right)_{min}=16\) khi \(a=1\)
Vậy khi tọa độ M là \(M\left(1;1\right)\) thì diện tích tam giác MAB nhỏ nhất

A và B là điểm nào nhỉ? Không thấy có mặt trong giả thiết?

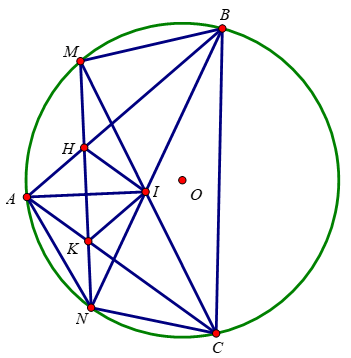
a) Xét tứ giác HMBI có:
∠HMI = ∠HBI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AN}=\widebat{CN}\))
Mà 2 góc này cùng nhìn cạnh HI
=> Tứ giác BMHI nội tiếp
b) Xét ΔMNI và ΔMKC có:
∠KMC là góc chung
∠MNI = ∠KCM (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{BM}\))
=> ΔMNI ∼ ΔMCK => \(\frac{MN}{MC}=\frac{MI}{MK}\) => MN.MK = MC.MI
c) Xét tứ giác NKIC có:
∠KNI = ∠KCI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{MB}\))
Mà 2 góc này cùng nhìn cạnh KI
=> Tứ giác NKIC là tứ giác nội tiếp
=> ∠NKI + ∠NCI = 180o (1)
Xét đường tròn (O) có:
\(\hept{\begin{cases}\widehat{ANK}=\widehat{ACM}\left(\text{2 góc nội tiếp cùng chắn cung AM}\right)\\\widehat{NAK}=\widehat{NCA}\left(\text{2 góc nội tiếp cùng chắn 2 cung BẰNG NHAU}\widebat{AN}=\widebat{CN}\right)\end{cases}}\)
=> ∠ANK + ∠NAK = ∠ACM + ∠NCA = ∠NCI (2)
Xét tam giác AKN có: ∠ANK + ∠NAK + ∠NKA = 180o (3)
Từ (1), (2), (3) => ∠NKI = ∠NKA
Xét tam giác IKN và tam giác AKN có:
∠NKI = ∠NKA
KN là cạnh chung
∠KNI = ∠KNA (2 góc nội tiếp chắn 2 cung bằng nhau)
=> ΔIKN = ΔAKN
=> IK=AK =>ΔAKI cân tại K
Tứ giác NKIC là tứ giác nội tiếp
Mặt khác ∠KCN = ∠ABN (2 góc nội tiếp cùng chắn cung AN của (O))
∠BAC = ∠BNC (2 góc nội tiếp cùng chắc cung BC của (O))
=> Tứ giác AHIK là hình bình hành
Mà IK = AK
=> Tứ giác AHIK là hình thoi.
CÒN LẠI TỰ LÀM LÀM NHA

Xét phương trình: \(x^2-2x+3=x+7\Leftrightarrow\orbr{\begin{cases}x=4\\x=-1\end{cases}}\)
Suy ra \(d\) cắt \(\left(P\right)\) tại hai điểm \(A\left(4;11\right)\) và \(B\left(-1;6\right)\)
Giả sử \(M\left(x_0;y_0\right)\) thay đổi trên cung AB của \(\left(P\right)\). Dễ thấy \(x_0\in[-1;4]\)
Vì \(M\in\left(P\right)\) nên \(M\left(x_0;x_0^2-2x_0+3\right)\)
Ta có \(d\left(M,AB\right)=d\left(M,d\right)=\frac{\left|x_0-\left(x_0^2-2x_0+3\right)+7\right|}{\sqrt{2}}=\frac{\left|-x_0^2+3x_0+4\right|}{\sqrt{2}}=f\left(x_0\right)\)
Chú ý rằng \(x_0\in[-1;4]\), suy ra \(d\left(M,AB\right)=f\left(x_0\right)\le f\left(\frac{3}{2}\right)=\frac{25\sqrt{2}}{8}\)
Khi đó \(S_{MAB}=\frac{1}{2}d\left(M,AB\right).AB\le\frac{1}{2}.\frac{25\sqrt{2}}{8}.\sqrt{\left(-1-4\right)^2+\left(6-11\right)^2}=\frac{125}{8}\)
Đạt được khi \(M\left(\frac{3}{2};\frac{9}{4}\right).\)

Cách 1. Suy luận.
Điểm M nằm ở góc phần tư thứ IV nên điểm M 1 nằm ở góc phần tư thứ hai. Số đo A M 1 dương nên hai phương án A, D bị loại. Mặt khác sđ A M 1 < 180 o nên phương án B bị loại.
Vậy đáp án là C.
Cách 2. Tính trực tiếp.
Gọi B là giao điểm của đường phân giác góc xOy với đường tròn. Ta có
Sđ A B = 45 o , s đ M A = 70 o
Suy ra sđ MB = 115 o .
Mà sđ B M 1 = sđ MB nên sđ A M 1 = 45 o + 115 o = 160 o .
Đáp án: C

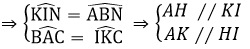
Gọi \(M\left(m^2;m\right)\) với \(-1< m< 3\)
\(\Rightarrow S_{MAB}=\dfrac{1}{2}\left|\left(x_M-x_A\right)\left(y_B-y_A\right)-\left(x_B-x_A\right)\left(y_M-y_A\right)\right|\)
\(=\dfrac{1}{2}\left|4\left(m^2-1\right)-8\left(m+1\right)\right|=2\left|m^2-2m-3\right|\)
Do \(m^2-2m-3< 0;\forall m\in\left(-1;3\right)\)
\(\Rightarrow S=-2\left(m^2-2m-3\right)=8-2\left(m-1\right)^2\le8\)
Dấu "=" xảy ra khi \(m=1\) hay \(M\left(1;1\right)\)