Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\)vectơ \(\overrightarrow c = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b \) có độ dài gấp \(\frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}\) lần vectơ \(\overrightarrow b \) và cùng hướng với vectơ \(\overrightarrow b \)
+) Nếu hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)cùng hướng và ngược lại
+) \(\left| {\overrightarrow c } \right| = \left| {\frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b } \right| = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\left| {\overrightarrow b } \right| = \left| {\overrightarrow a } \right|\). Suy ra hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)có cùng độ dài

Lời giải:
Xét hai vecto bất kỳ \(\overrightarrow{AB}, \overrightarrow{CD}\). Kẻ vecto $\overrightarrow{CT}$ sao cho $\overrightarrow{CT}=\overrightarrow{BA}$
Ta có:
\(|\overrightarrow{AB}+\overrightarrow{CD}|=|\overrightarrow{TC}+\overrightarrow{CD}|=|\overrightarrow{TD}|\)
\(|\overrightarrow{AB}|+|\overrightarrow{CD}|=|\overrightarrow{TC}|+|\overrightarrow{CD}|\)
Mà theo bđt tam giác thì:
\(|\overrightarrow{TC}+\overrightarrow{CD}|\geq |\overrightarrow{TD}|\Rightarrow |\overrightarrow{AB}|+\overrightarrow{CD}|\geq |\overrightarrow{AB}+\overrightarrow{CD}|\)
Dấu "=" xảy ra khi \(T, C,D\) thẳng hàng và $C$ nằm giữa $T,D$
$\Leftrightarrow \overrightarrow{TC}, \overrightarrow{CD}$ cùng hướng
$\Leftrightarrow \overrightarrow{AB}, \overrightarrow{CD}$ cùng hướng
Vậy với $\overrightarrow{a}, \overrightarrow{b}$ bất kỳ thì $|\overrightarrow{a}|+|\overrightarrow{b}|\geq |\overrightarrow{a}+\overrightarrow{b}|$. Dấu "=" xảy ra khi $\overrightarrow{a}, \overrightarrow{b}$ cùng hướng.
------------------
Áp dụng vào bài toán:
\(|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|\leq |\overrightarrow{a}+\overrightarrow{b}|+|\overrightarrow{c}|\leq |\overrightarrow{a}|+|\overrightarrow{b}|+|\overrightarrow{c}|\)
Dấu "=" xảy ra khi \(\overrightarrow{a}, \overrightarrow{b}\) cùng hướng và \(\overrightarrow{a}+\overrightarrow{b}, \overrightarrow{c}\) cùng hướng
\(\Leftrightarrow \overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}\) cùng hướng

a: Đặt \(\overrightarrow{a}=\overrightarrow{AB};\overrightarrow{BC}=\overrightarrow{b}\)
\(\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|=\left|\overrightarrow{AB}\right|+\left|\overrightarrow{BC}\right|\)=AB+BC
|vecto a+vecto b|=|vecto AB+vecto BC|=AC
AB+BC=AC
=>A,B,C thẳng hàng
=>vecto AB và vecto BC cùng hướng
c: |vecto a+vecto b|=|vecto a-vecto b|
=>vecto a+vecto b=vecto a-vecto b hoặc vecto a+vecto b=vecto b-vecto a
=>vecto b=vecto0 hoặc vecto a=vecto 0

a) cos(;
) =
= 0
=> (;
) = 900
b) cos(;
) =
=
=> (;
) = 450
c) cos(;
) =
=
=> (;
) = 1500
Đăng những câu khác đi em mỏi tay rồi

\(\left|\overrightarrow{a}+\overrightarrow{b}\right|^2=\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)\)
\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\overrightarrow{a}.\overrightarrow{b}\)
\(=5^2+12^2+2.5.12.cos\left(\overrightarrow{a},\overrightarrow{b}\right)\)
\(=169+120cos\left(\overrightarrow{a},\overrightarrow{b}\right)=13^2\)
Suy ra: \(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=0\).
\(\overrightarrow{a}\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left(\overrightarrow{a}\right)^2+\overrightarrow{a}.\overrightarrow{b}=5^2+5.12.0=25\).
Mặt khác \(\overrightarrow{a}\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left|\overrightarrow{a}\right|.\left|\overrightarrow{a}+\overrightarrow{b}\right|.cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)\)
\(=5.13.cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)\).
Vì vậy \(25=5.13.cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)\).
\(cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)=\dfrac{5}{13}\).
Vậy góc giữa hai véc tơ \(\overrightarrow{a}\) và \(\overrightarrow{a}+\overrightarrow{b}\) là \(\alpha\) sao cho \(cos\alpha=\dfrac{5}{13}\).

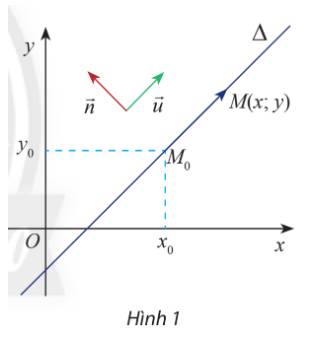
a) Ta có \(\overrightarrow n .\overrightarrow u = a.b + b.( - a) = 0\)
Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau
b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)
=> luôn cùng phương với vectơ \(\overrightarrow u \)
=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)

a) \(\overrightarrow{a}+\overrightarrow{b}=\left(2;-2\right)+\left(1;4\right)=\left(3;2\right)\).
\(\overrightarrow{a}-\overrightarrow{b}=\left(2;-2\right)-\left(1;4\right)=\left(1;-6\right)\).
\(2\overrightarrow{a}+3\overrightarrow{b}=2\left(2;-2\right)+3\left(1;4\right)=\left(4;-4\right)+\left(3;12\right)\)\(=\left(7;8\right)\).
c) Gọi x và y là hai số thực để:
\(\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}=x\left(2;-2\right)+y\left(1;4\right)=\left(2x+y;-2x+4y\right)\)
Từ đó suy ra: \(\left\{{}\begin{matrix}2x+y=5\\-2x+4y=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\).
Vậy \(\overrightarrow{c}=2\overrightarrow{a}+1\overrightarrow{b}\).
a) \(\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \Leftrightarrow {\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left( {\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|} \right)^2}\)
\( \Leftrightarrow {\left( {\overrightarrow a + \overrightarrow b } \right)^2} = {\left( {\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|} \right)^2} \Leftrightarrow {\left( {\overrightarrow a } \right)^2} + 2\overrightarrow a .\overrightarrow b + {\left( {\overrightarrow b } \right)^2} = {\left| {\overrightarrow a } \right|^2} + 2.\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| + {\left| {\overrightarrow b } \right|^2}\)
\( \Leftrightarrow {\left| {\overrightarrow a } \right|^2} + 2\overrightarrow a .\overrightarrow b + {\left| {\overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + 2.\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| + {\left| {\overrightarrow b } \right|^2}\)
\( \Leftrightarrow 2\overrightarrow a .\overrightarrow b = 2\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\)
\( \Leftrightarrow 2\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 2\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\)
\( \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 1 \Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 0^\circ \)
Vậy \(\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \Leftrightarrow \overrightarrow a , \,\overrightarrow b \) cùng hướng.
b) \(\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a - \overrightarrow b } \right| \Leftrightarrow {\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a - \overrightarrow b } \right|^2}\)
\( \Leftrightarrow {\left( {\overrightarrow a + \overrightarrow b } \right)^2} = {\left( {\overrightarrow a - \overrightarrow b } \right)^2}\)
\( \Leftrightarrow {\left( {\overrightarrow a } \right)^2} + 2\overrightarrow a .\overrightarrow b + {\left( {\overrightarrow b } \right)^2} = {\left( {\overrightarrow a } \right)^2} - 2\overrightarrow a .\overrightarrow b + {\left( {\overrightarrow b } \right)^2}\)
\( \Leftrightarrow 2\overrightarrow a .\overrightarrow b = - 2\overrightarrow a .\overrightarrow b \Leftrightarrow 4\overrightarrow a .\overrightarrow b = 0\)
\( \Leftrightarrow \overrightarrow a .\overrightarrow b = 0 \Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \)
Vậy \(\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a - \overrightarrow b } \right| \Leftrightarrow \overrightarrow a ,\overrightarrow b \) vuông góc với nhau.