Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vì Đường tròn (O;R) có đường kính BC cắt AB, AC lần lượt là F và E => góc HEA = góc HFA = 90o
mà hai góc này là hai góc đối nhau=> tứ giác AFHE nội tiếp

△ABC nội tiếp đường tròn đường kính BC.
\(\Rightarrow\)△ABC vuông tại A.
- Ta có: \(\widehat{ABC}+\widehat{ABG}=90^0\) (\(BG\perp BC\) tại B).
\(\widehat{EBG}+\widehat{ABG}=90^0\) (\(AB\perp EB\) tại B).
\(\Rightarrow\widehat{ABC}=\widehat{EBG}\)
△ABC và △EBG có: \(\widehat{ABC}=\widehat{EBG}\) (cmt)
\(AB=EB\) (ABED là hình vuông).
\(\widehat{BAC}=\widehat{BEG}=90^0\)
\(\Rightarrow\)△ABC=△EBG (g-c-g).
\(\Rightarrow\widehat{ACB}=\widehat{EGB}\) (1).
AFBC là tứ giác nội tiếp có \(\widehat{EFB}\) là góc ngoài đỉnh F.
\(\Rightarrow\widehat{ACB}=\widehat{EFB}\) (2).
(1), (2) \(\Rightarrow\widehat{EGB}=\widehat{EFB}\) nên GEBF nội tiếp.

a) góc BED nội tiếp chắn nửa đg tròn đg kính BD => góc BED =900 hay góc BEC =900
=> góc BEC = góc BAC = 900 => tứ giác ACBE nội tiếp đg tròn đg kính BC, tâm G là trung điểm BC
b) tứ giác ACBE nội tiếp => góc ABC = góc AEC (1)
mặt khác B,D,E,F thuộc đg tròn đg kính BD => BDEF là tứ giác nội tiếp => góc AED = góc DBF (góc ngoài bằng góc đối trog)
hay góc AEC = góc ABF (2)
từ (1) và (2) => đpcm
c) trog (G) góc AGB = 2 góc ACB (góc nội tiếp và góc ở tâm) => góc AGB = 1200 => sđ cung AB = 1200
mặt khác tam giác AGC đều nên GA =3cm
từ đó bn tính đc S quạt AGBA = \(27\pi\left(cm^2\right)\)

a, Xét tứ giác BEHF có: góc BFH + góc BEH = 900 + 900 = 1800
=> Tứ giác BEHF nội tiếp.
b, Xét tứ giác AFEC có :
góc AFC = góc AEC ( = 900) (Hai góc cùng nhìn 1 cạnh dưới 1 góc vuông)
=> Tứ giác AFEC nội tiếp
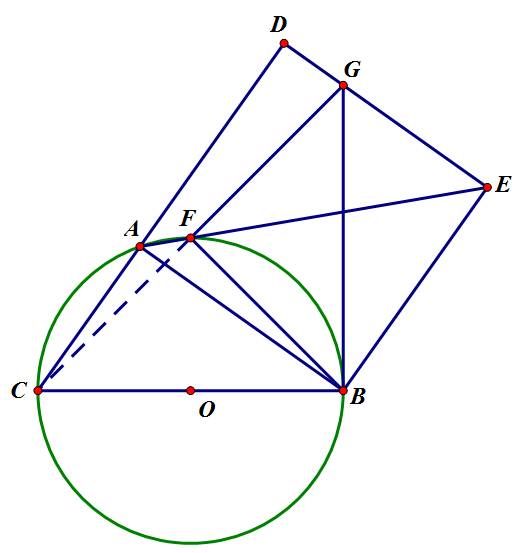
góc GDC=góc GBC=90 => tứ giác nội típ
I là trung điểm của GC
BFC vuông cân niềm tin ak