Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

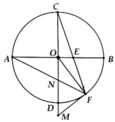
a, Học sinh tự chứng minh
b, Chứng minh: A F M ^ = C A F ^ ( = A C F ^ ) => MF//AC
c, Chứng minh: M F N ^ = M N F ^ => ∆MNF cân tại M => MN = MF
Mặt khác: OD = OF = R
Ta có MF là tiếp tuyến nên DOFM vuông => ĐPCM

a: góc ACB=1/2*180=90 độ
=>AC vuông góc BE
góc AME+góc ACE=180 độ
=>AMEC nội tiếp
b: Xét ΔBCA vuông tại C và ΔBME vuông tại M có
góc CBA chung
=>ΔBCA đồng dạng với ΔBME
=>BC/BM=BA/BE
=>BE*BA=BM*BA=3R*2R=6R^2

Chứng minh có bạn câu a,b trước. Câu c tìm không ra tam giác ~ . Chưa ra cách khác
(Vẽ đẹp hơn rồi kk)
a/ Ta có \(\widehat{AEB}=90\)độ (Góc nội tiếp chắn nửa đường tròn)
Xét tứ giác \(BEHF\)có: \(\hept{\begin{cases}\widehat{AEB}=90\left(cmt\right)\\\widehat{FHB}=90\left(gt\right)\end{cases}}\)
\(\Rightarrow\widehat{AEH}+\widehat{FHB}=90+90=180\)độ
\(\Rightarrow\)Tứ giác \(BEHF\)nội tiếp
b/ (Nối giùm mình K với A)
Ta có: \(\widehat{KEA}=\widehat{KBA}\)( Tứ giác \(KEAB\)nt, cùng chắn \(\widebat{AK}\))
Mà: \(\widehat{AEH}=\widehat{KBA}\)( Tứ giác \(BEHF\)nt, cùng chắn \(\widebat{FH}\))
\(\Rightarrow\widehat{KEA}=\widehat{AEH}\)
\(\RightarrowĐpcm\)
*Kẻ OI ⊥ EM, OH ⊥ FM. (1)
Theo đề, ta có AB=CD, AE=BM, CF=DM
Mà AI+EA=EI, IB+BM=IB và MD+DH=MH, HC+CF=HF
=>EM=MF (2)
Từ (1) và (2), suy ra:
IO=OH (định lí giữa dây và khoảng cách từ tâm đến dây)(3)
EI=IM, MH=HF(định lí đường kính và dây) => EI=IM=MH= HF (4)
Xét △EOI và △FOH, có:
EI=FH (theo (4)) , góc EIO= góc FHO (=90o)
IO=OH (theo(3))
=> △EIO=△FOH (c.g.c)
Do đó: OE=OF ( 2 cạnh tương ứng)
Vậy OE=OF (đpcm)
HAVE A GOOD DAY!