Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mk không biết tải hình lên, xin lỗi bn nhé.
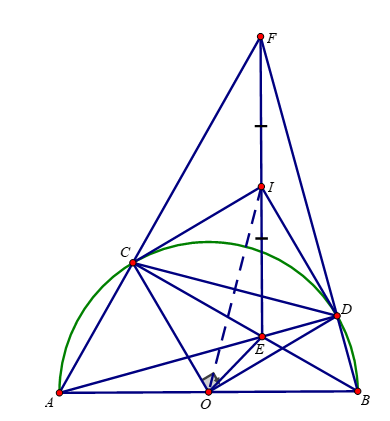
a) Do AB là đường kính của (O) nên
\(\Rightarrow\widehat{ACB}=\widehat{ADB}=90^0\)
Xét tứ giác CEDF có : \(\widehat{ECF}+\widehat{EDF}=180^0\)
\(\Rightarrow ECDF\)là tứ giác nội tiếp (ĐPCM)
b) Do \(\widehat{ECF}=\widehat{EDF}=90^0\)nên ECDF nội tiếp đường tròn đường kính EF
Hay ECDF nội tiếp (I;IE) nên
\(\widehat{IDF}=\widehat{IFD}=\widehat{ECD}=\frac{1}{2}sđ\widebat{BD}=\widehat{OAD}=\widehat{ODA}\)
Từ đó ta có: \(\widehat{IDO}=\widehat{IDE}+\widehat{OAD}=\widehat{IDE}+\widehat{IDF}=90^0\)
\(\Rightarrow\)ID là tiếp tuyến của đường tròn (O) (ĐPCM)

a) ∠ACB = 90o (góc nội tiếp chắn nửa đường tròn)=>∠FCE = 90o
∠ADB = 90o (góc nội tiếp chắn nửa đường tròn)=>∠FDE = 90o
Xét tứ giác CEDF có:
∠FCE = 90o
∠FDE = 90o
=> ∠FCE + ∠FDE = 180 o
=> Tứ giác CEDF là tứ giác nội tiếp
b) Xét ΔAFD và ΔBFC có:
∠AFB là góc chung
∠ADF = ∠BCF = 90o
=> ΔAFD ∼ ΔBFC
\(\Rightarrow\frac{FA}{FB}=\frac{FD}{FC}\)=> FA.FC = FB.FD
c) Do ∠FCE = 90oNên FE là đường kính đường tròn ngoại tiếp tứ giác CEDF
Do đó trung điểm I của FE là tâm đường tròn ngoại tiếp tứ giác CEDF
Tam giác CFI có IC = IF => ΔCFI cân tại I
=> CFI = ∠FCI
Tứ giác CEDF nội tiếp =>∠CFI = CDE (2 góc nội tiếp cùng chắn \(\widebat{EC}\))
Tứ giác ACDB nội tiếp =>∠CDE = ∠CBA(2 góc nội tiếp cùng chắn \(\widebat{AC}\))
ΔAOB cân tại O =>∠BCO = ∠CBA
=> ∠FCI = ∠BCO
=> ∠FCI + ∠ECI = ∠BCO + ∠ECI <=> ∠FCE = ∠ICO
=> ∠ICO = 90o
Vậy IC là tiếp tuyến của (O)
d) Chứng minh tương tự câu c, ta có ∠IDO) = 90o
Xét tứ giác ICOD có:
∠ICO = ∠IDO = ∠COD = 90o
=> Tứ giác ICOD là hình chữ nhật
Lại có OC = OD = R
=> Tứ giác ICOD là hình vuông.
Có OI là đường chéo hình vuông cạnh R
=> OI = R√2
O cố định, do đó I thuộc đường tròn tâm O, bán kính R√2 cố định
HÌNH THÌ VÀO THỐNG KÊ NHA

a: góc ACB=1/2*180=90 độ
=>góc FCE=90 độ
góc ADB=1/2*180=90 độ
=>gó FDE=90 độ
Vì góc FCE+góc FDE=180 độ
nên FCED nội tiếp
b: Đề sai rồi bạn vì F,C,A thẳng hàng
c: góc ICO=góc ICE+góc OCE
=góc IEC+góc OBE
=90 độ-góc CBA+góc CBA
=90 độ
=>CI là tiếp tuyến của (O)

a: góc ACB=1/2*180=90 độ
=>góc FCE=90 độ
góc ADB=1/2*180=90 độ
=>gó FDE=90 độ
Vì góc FCE+góc FDE=180 độ
nên FCED nội tiếp
b: Đề sai rồi bạn vì F,C,A thẳng hàng
c: góc ICO=góc ICE+góc OCE
=góc IEC+góc OBE
=90 độ-góc CBA+góc CBA
=90 độ
=>CI là tiếp tuyến của (O)
COD= 90 độ nha