Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu này hơi kì, vì đề đã nói rõ tiếp tuyến cắt Oz tại M, thế thì M chạy trên tia Oz còn hỏi gì nữa???
mình nghĩ câu này, nên "giấu" cái Oz đi, mà cho M là trung điểm của CD, làm thế nhé
Thấy tứ giác ABDC là hình thang vuông, có OM là đường trung bình (qua trung điểm 2 cạnh bên)
=> OM // Ax // By => M chạy trên tia qua O và // Ax (chính là Oz)

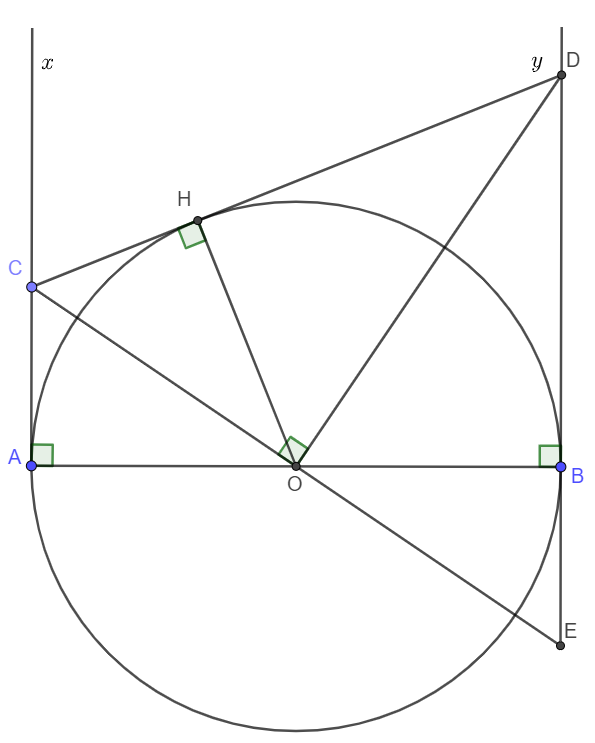
Vẽ OH\perp CD\left(H\in CD\right)OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có \Delta OAC=\Delta OBE\left(g.c.g\right)\Rightarrow OC=OEΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH\perp DC,OB\perp DE\Rightarrow OH=OB.OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH\perp CD,OH=OB=rOH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).
Vẽ OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có ΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).

A B E F x y M K O
a)\(\hept{\begin{cases}Ax⊥AB\\By⊥AB\end{cases}}\)=> Ax // By.\(\Delta KFB\)có EA // FB nên\(\frac{KF}{KA}=\frac{BF}{AE}\)(hệ quả định lí Ta-lét) mà EA = EM ; FM = FB (tính chất của 2 tiếp tuyến)
\(\Rightarrow\Delta AEF\)có\(\frac{KF}{KA}=\frac{MF}{ME}\)nên MK // AE (định lí Ta-lét đảo) mà\(AE⊥AB\Rightarrow MK⊥AB\)
b)\(\widehat{EOM}=\frac{\widehat{AOM}}{2};\widehat{FOM}=\frac{\widehat{MOB}}{2}\)(tính chất 2 tiếp tuyến) mà\(\widehat{EOM}+\widehat{FOM}=180^0\)(kề bù)
\(\Rightarrow\widehat{EOF}=\widehat{EOM}+\widehat{FOM}=\frac{180^0}{2}=90^0\)
\(\Rightarrow\Delta EOF\)vuông tại O có OE + OF > EF (bđt tam giác) ; OE + OF < 2EF (vì OE,OF < EF)
\(\Rightarrow1< \frac{OE+OF}{EF}< 2\Rightarrow2< \frac{P_{EOF}}{EF}< 3\Rightarrow\frac{1}{3}< \frac{EF}{P_{EOF}}< \frac{1}{2}\)(1)
Hình thang AEFB (AE // FB) có diện tích là :\(\frac{\left(AE+FB\right).AB}{2}=\frac{\left(EM+FM\right).2R}{2}=EF.R\)
SAEO = SMEO vì có đáy OA = OM ; đường cao AE = ME\(\Rightarrow S_{MEO}=\frac{1}{2}S_{AEMO}\)
SFOM = SFOB vì có đáy FM = FB ; đường cao OM = OB\(\Rightarrow S_{FOM}=\frac{1}{2}S_{MFBO}\)
\(\Rightarrow S_{EOF}=\frac{1}{2}\left(S_{AEMO}+S_{MFBO}\right)=\frac{EF.R}{2}\).Từ tâm đường tròn nội tiếp I của\(\Delta EOF\)kẻ các đường vuông góc với OE,OF,EF thì\(S_{EOF}=S_{EIF}+S_{EIO}+S_{OIF}\)\(\Leftrightarrow\frac{EF.R}{2}=\frac{EF.r+EO.r+OF.r}{2}\)
\(\Rightarrow EF.R=P_{EOF}.r\Rightarrow\frac{r}{R}=\frac{EF}{P_{EOF}}\)(2).Thay (2) vào (1) ta có đpcm.
0 A B X Y E C D M 1 2 1 2
đANG VIẾT DỞ kích nhầm :)) tiếp nè :
Nối \(EH\)ta có phương \(MOBD\)Nội tiếp đường tròn tâm \(H\)Bán kính là \(OH\)có phương tích từ \(E\)Đến đường tròn \(\left(H\right)\)
\(\hept{\begin{cases}EM.ED=EH^2-OH^2\\EO.EB=EH^2-OH^2\end{cases}\Rightarrow EM.ED=EO.EB}\)