Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
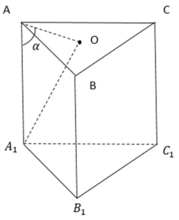
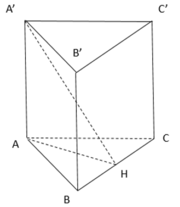
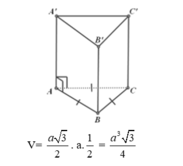
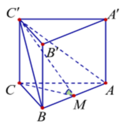
Gọi H là trọng tâm tam giác đều ABC có diện tích S A B C = a 3 2
A 1 cách đều A, B, C
![]()
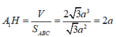
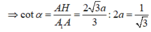
⇒ α = 60 o

Để tính toán có thể phân tích khối A'.BCC'B', ta có thể sử dụng công thức: V = (1/3) * S * h, trong đó V là có thể phân tích, S là đáy phân tích và h là chiều high of the block.
Trước tiên, ta cần tính diện tích đáy S. Với diện tích tam giác đều A'ABC, diện tích đáy là diện tích tam giác ABC. Ta có công thức tính diện tích tam giác đều là S = (a^2 * √3) / 4.
Giờ ta cần tính chiều cao h. Theo đề bài, cosα = 1/√3. Chúng ta biết rằng cosα = h/AB = h/a. Từ đó suy ra h = a/√3.
Tiếp theo, ta thay vào công thức thể tích V = (1/3) * S * h:
V = (1/3) * ((a^2 * √3)/4) * (a / √3)
= (a^3 * √3) / (12√3)
= a^3 / 12
Do đó, có thể phân bổ khối A'.BCC'B' là a^3/12.
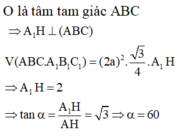
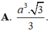
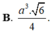
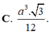
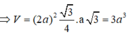
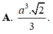
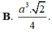
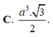
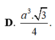

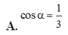
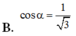
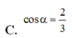
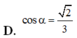
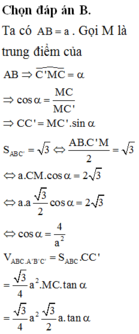
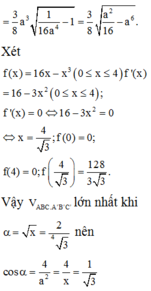

Chọn A