Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

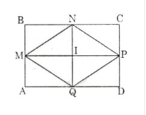
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh là M, N, P, Q.
Vẽ tứ giác MNPQ

Lại có: ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2) và (3) suy ra: MN = PQ = MQ = NP
=> Tứ giác MNPQ là hình thoi.
+ Ta có:
∆ BMN = ∆ IMN; ∆ INP = ∆ CNP, ∆ AMQ= ∆IMQ, ∆ DPQ= ∆IPQ
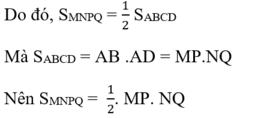
Như vậy diện tích hình thoi bằng nửa tích hai đường chéo.

Cho hình thoi MNPQ, vẽ hình chữ nhật có một cạnh là đường chéo MP, cạnh kia bằng IN ( IN= 1212 NQ).
Khi đó diện tích của hình chữ nhật MPBA bằng diện tích hình thoi MNPQ.
Thật vậy SMPBA = MP. IN = MP. 1212 NQ
= 1212 MP. NQ = SMNPQ


Cho hình thoi MNPQ, vẽ hình chữ nhật có một cạnh là đường chéo MP, cạnh kia bằng IN ( IN= NQ).
Khi đó diện tích của hình chữ nhật MPBA bằng diện tích hình thoi MNPQ.
Thật vậy SMPBA = MP. IN = MP. NQ
= MP. NQ = SMNPQ
Cho hình thoi MNPQ, vẽ hình chữ nhật có một cạnh là đường chéo MP, cạnh kia bằng IN ( IN= NQ).
Khi đó diện tích của hình chữ nhật MPBA bằng diện tích hình thoi MNPQ.
Thật vậy SMPBA = MP. IN = MP. NQ
= MP. NQ = SMNPQ

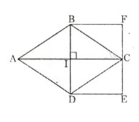
Cho hình thoi ABCD, vẽ hình chữ nhật có một cạnh là đường chéo BD, cạnh kia bằng IC (bằng nửa AC).
Khi đó diện tích của hình chữ nhật BDEF bằng diện tích hình thoi ABCD.
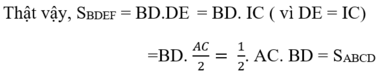
Từ đó suy ra cách tính diện tích hình thoi: Diện tích hình thoi bằng nửa tích hai đường chéo.

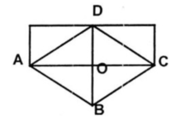
Giả sử ta có hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Ta cắt hình thoi theo đường chéo AC ta được 2 tam giác.
Lấy AC làm một cạnh hình chữ nhật. Cắt tam giác BAC theo đường BO ta được hai tam giác ghép lại ta có hình chữ nhật.

a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: Để mNPQ là hình chữ nhật thì MN vuông góc với MQ
=>AC vuông góc với BD
Để MNPQ là hình thoi thì MN=MQ
=>AC=BD
c: BD=3/2*AC=30cm
=>MQ=BD/2=15cm; MN=AC/2=10cm
SMNPQ=15*10=150cm2
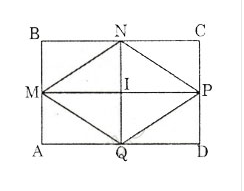
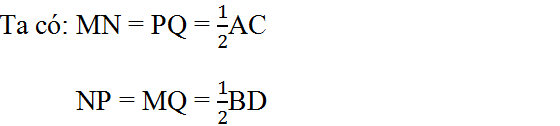
Cho hình chữ nhật ABCD; M,N,P,Q lần lượt là trung điểm của AB,BC, CD, DA.
* Chứng minh MNPQ là hình thoi
Ta có MN = PQ = 1/2BD
NP = MQ = 1/2 AC
Mà AC = BD
⇒ MN = NP = PQ = QM nên tứ giác MNPQ là hình thoi (Có 4 cạnh bằng nhau)
* Theo bài 33 (các em tham khảo ở trên), ta có SMNPQ = SABNQ và SMNPQ = SNQDC
Vì vậy SABCD = SABNQ + SNQDC = 2SMNPQ
* Ta có SABCD =2SMNPQ ⇒ SMNPQ = 1/2SABCD = 1/2AB.BC = 1/2NQ.MP
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh M, N, P, Q.
Vẽ tứ giác MNPQ
Ta có MN = PQ = \(\dfrac{1}{2}\)BD
NP = MQ = \(\dfrac{1}{2}\) AC
Mà AC = BD
Nên tứ giác MNPQ là hình thoi vì có bốn cạnh bằng nhau.
Dễ dàng chứng minh rằng : ∆AMN = ∆INM , ∆BPN = ∆NIP
∆PCQ = ∆IQP, ∆DMQ = IQM
Do đó
SMNPQ = \(\dfrac{1}{2}\) SABCD mà SABCD = AB. AD = MP. NQ
Vậy SMNPQ = \(\dfrac{1}{2}\) MP.NQ