Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(3x-2^4\right).7^3=2.7^4\)\(\Leftrightarrow3x-2^4=2.7^4:7^3\)
\(\Leftrightarrow3x-16=2.7\)\(\Leftrightarrow3x-16=14\)\(\Leftrightarrow3x=30\)
\(\Leftrightarrow x=10\)
Vậy \(x=10\)
b) \(3x+4x=\left|-75\right|+23\)\(\Leftrightarrow7x=75+23\)
\(\Leftrightarrow7x=98\)\(\Leftrightarrow x=14\)
Vậy \(x=14\)
a) \(\left(3x-2^4\right)\cdot7^3=2\cdot7^4\)
=> \(3x\cdot7^3-2^4\cdot7^3=2\cdot7\cdot7^3\)
=> \(3x\cdot7^3=14\cdot7^3+16\cdot7^3\)
=> \(3x\cdot7^3=\left(14+16\right)\cdot7^3\)
=> \(3x\cdot7^3=30\cdot7^3\)
=> \(3x=30\)(bỏ hai vế 73)
=> \(x=10\)
Vậy x = 10
b) \(3x+4x=\left|-75\right|+23\)
=> \(7x=75+23\)
=> \(7x=98\)
=> \(x=14\)
Vậy x = 14

a) \(\dfrac{x}{5}+\dfrac{1}{2}=\dfrac{6}{10}\\ \dfrac{x}{5}+\dfrac{1}{2}=\dfrac{3}{5}\\ \dfrac{x}{5}=\dfrac{3}{5}-\dfrac{1}{2}\\ \dfrac{x}{5}=\dfrac{6}{10}-\dfrac{5}{10}\\ \dfrac{x}{5}=\dfrac{1}{10}\\ \dfrac{2x}{10}=\dfrac{1}{10}\\ \Rightarrow2x=1\\ x=1:2\\ x=0,5=\dfrac{1}{2}\)
b) \(x+\dfrac{3}{15}=\dfrac{1}{3}\\ x=\dfrac{1}{3}-\dfrac{3}{15}\\ x=\dfrac{5}{15}-\dfrac{3}{15}\\ x=\dfrac{2}{15}\)
c) \(x-\dfrac{12}{4}=\dfrac{1}{2}\\ x-3=\dfrac{1}{2}\\ x=\dfrac{1}{2}+3\\ x=\dfrac{1}{2}+\dfrac{6}{2}\\ x=\dfrac{7}{2}\)
d) \(\dfrac{1}{2}x+\dfrac{1}{2}=\dfrac{5}{2}\\ \dfrac{1}{2}x=\dfrac{5}{2}-\dfrac{1}{2}\\ \dfrac{1}{2}x=2\\ x=2:\dfrac{1}{2}\\ x=4\)
a. \(\dfrac{2x+5}{10}=\dfrac{6}{10}\Leftrightarrow2x=1\Leftrightarrow x=\dfrac{1}{2}\)
b. \(\dfrac{15x+3}{15}=\dfrac{5}{15}\Leftrightarrow15x=2\Leftrightarrow x=\dfrac{2}{15}\)
c. \(\dfrac{4x-12}{4}=\dfrac{2}{4}\Leftrightarrow4x=14\Leftrightarrow x=\dfrac{7}{2}\)
d. \(\dfrac{1+x}{2x}=\dfrac{5x}{2x}\Leftrightarrow-4x=-1\Leftrightarrow x=\dfrac{1}{4}\)
e. \(\dfrac{-4\left(2x-5\right)}{6\left(2x-5\right)}-\dfrac{2}{6\left(2x-5\right)}=\dfrac{9\left(2x-5\right)}{6\left(2x-5\right)}\)
\(\Leftrightarrow-8x+20-2=18x-45\)
\(\Leftrightarrow-26x=-63\Leftrightarrow x=\dfrac{63}{26}\)

\(\left(x-1\right)^3-2\left(x+1\right)^2=\left(2x+1\right)\left(1-3x\right)-2x\left(1-x\right)\)
\(\Leftrightarrow x^3-3x^2+3x-1-2x^2-4x-2=2x-6x^2+1-3x-2x+2x^2\)
\(\Leftrightarrow x^3-5x^2-x-3=-4x^2-3x+1\)
\(\Leftrightarrow x^3+x^2+2x-4=0\)
\(\Leftrightarrow x^3-x^2+2x^2-2x+4x-4=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2x+4\right)=0\)
=>x-1=0
hay x=1

\(\dfrac{\left(44.52.60\right)}{11.13.15}=\dfrac{44}{11}\cdot\dfrac{52}{13}\cdot\dfrac{60}{15}=4.4.4=64\)

a) 1/2.x+3/5.(x-2)=3
<=>1/2.x+3/5.x-6/5=3
<=>11/10.x-6/5=3
<=>11/10x=41/10
<=>x=41/11
b) (3x-4).(5x+15)=0
<=>3x-4=0 hoặc 5x+15=0
<=>x=4/3 hoặc x=-3

Bài 1:
A = 32 + 33 + 34 + ... + 32018
3A = 33 + 34 + 35 + ... + 32019
3A - A = (33 + 34 + 35 + ... + 32019) - (32 + 33 + 34 + ... + 32018)
2A = 32019 - 9
A = (32019 - 9) : 2
= (32016.33 - 9) : 2
= [ (34)504.27 - 9] : 2
= [ (...1)504.27 - 9] : 2
= [ (...1).27 - 9] : 2
= [ (...7) - 9] : 2
= (....8) : 2
= ...4
Vậy c/s tận cùng của A là 4
Bài 2:
Ta có:
1019 + 1018 + 1017
= 1016.103 + 1016.102 + 1016.10
= 1016.(103 + 102 + 10)
= 1016.1110
= 1016.2.555
Vì 555 chia hết cho 555 nên 1016.2.555 chia hết cho 555
Vậy 1019 + 1018 + 1017 chia hết cho 555 (đpcm)
Bài 3:
x + 6 chia hết cho x + 2
=> x + 2 + 4 chia hết cho x + 2
=> 4 chia hết cho x + 2
=> x + 2 thuộc Ư(4) = {\(\pm1;\pm2;\pm4\)}
| x + 2 | 1 | -1 | 2 | -2 | 4 | -4 |
| x | -1 | -3 | 0 | -4 | 2 | -6 |
Vậy x = {-1;-3;0;-4;2;-6}
Bài 4:
Giả sử x + 4y chia hết cho 7 (1)
Vì 3x + 5y chia hết cho 7 nên 2(3x + 5y) chia hết cho 7
=> 6x + 10y chia hết cho 7 (2)
Từ (1) và (2) => (x + 4y) + (6x + 10y) chia hết cho 7
=> x + 4y + 6x + 10y chia hết cho 7
=> (x + 6x) + (4y + 10y) chia hết cho 7
=> 7x + 14y chia hết cho 7
=> 7(x + 2y) chia hết cho 7
=> Giả sử đúng
Vậy x + 4y chia hết cho 7 (đpcm)
Bài 5:
1, Ta có: \(-\left(x+2\right)^{2018}\le0\)
\(\Rightarrow-1-\left(x+2\right)^{2018}\le0\)
\(\Rightarrow A\le0\)
Dấu " = " xảy ra <=> (x + 2)2018 = 0 <=> x = -2
Vậy GTNN của A là -1 khi x = -2
2, Ta có: \(x^2\ge0\)
\(\left|2y-18\right|\ge0\)
\(\Rightarrow x^2+\left|2y-18\right|\ge0\)
\(\Rightarrow-9+x^2+\left|2y-18\right|\ge-9\)
Dấu " = " xảy ra <=> \(\left\{\begin{matrix}x^2=0\\\left|2y-18\right|=0\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix}x=0\\y=9\end{matrix}\right.\)
Vậy GTLN của B là -9 khi \(\left\{\begin{matrix}x=0\\y=9\end{matrix}\right.\)
Bài 6:
1, xy + 2x - y - 2 = 5
<=> x(y + 2) - (y + 2) = 5
<=> (x - 1)(y + 2) = 5
=> x - 1 và y + 2 thuộc Ư(5) = {\(\pm1;\pm5\)}
Ta có bảng:
| x - 1 | 1 | -1 | 5 | -5 |
| y + 2 | 5 | -5 | 1 | -1 |
| x | 2 | 0 | 6 | -4 |
| y | 3 | -7 | -1 | -3 |
Vậy các cặp (x;y) là (2;3) ; (0;-7) ; (6;-1) ; (-4;-3)
2, x + y = 2xy
<=> 2xy - x - y = 0
<=> 2(2xy - x - y) = 2.0
<=> 4xy - 2x - 2y = 0
<=> (4xy - 2x) - 2y - 1 = 0 - 1
<=> 2x(2y - 1) - (1 - 2y) = -1
<=> (2x - 1)(1 - 2y) = -1
=> 2x - 1 và 1 - 2y thuộc Ư(-1) = {\(\pm1\)}
Ta có bảng:
| 2x - 1 | 1 | -1 |
| 1 - 2y | -1 | 1 |
| x | 1 | 0 |
| y | 1 | 0 |
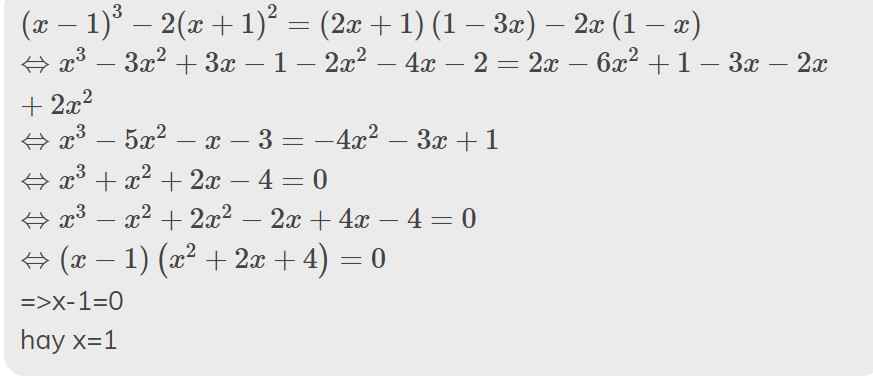
Tìm x ak
chắc j đó bn