Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
3-4*[(x-1)+(x+1)]=2x+1*1-3x-2x+1+x
-1x=2x-3x-2x+1+x
-1x=-3x+1+x
x+x-x=-3+1+1
x=-1
Mk làm luôn ko ghi đề bài
Mk ko chắc chắn lắm
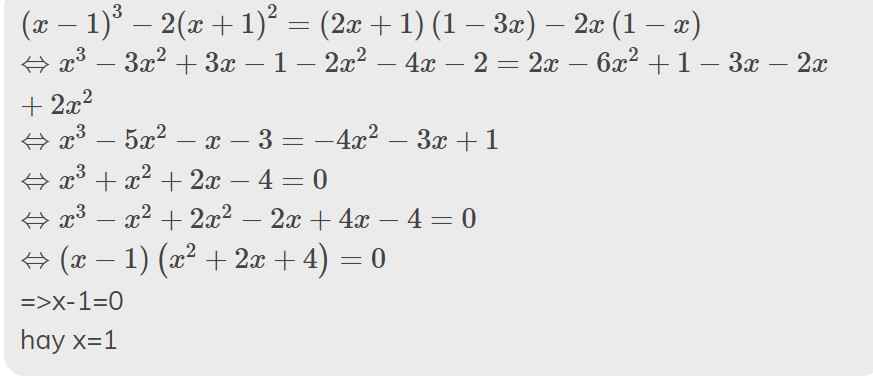
\(\left(x-1\right)^3-2\left(x+1\right)^2=\left(2x+1\right)\left(1-3x\right)-2x\left(1-x\right)\)
\(\Leftrightarrow x^3-3x^2+3x-1-2x^2-4x-2=2x-6x^2+1-3x-2x+2x^2\)
\(\Leftrightarrow x^3-5x^2-x-3=-4x^2-3x+1\)
\(\Leftrightarrow x^3+x^2+2x-4=0\)
\(\Leftrightarrow x^3-x^2+2x^2-2x+4x-4=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2x+4\right)=0\)
=>x-1=0
hay x=1
a)để -3/x-1 thuộc Z
=>-3 chia hết x-1
=>x-1\(\in\){1,-1,3,-3}
=>x\(\in\){2,0,4,-2}
b)để -4/2x-1 thuộc Z
=>4 chia hết 2x-1
=>2x-1\(\in\){1,-1,2,-2,4,-4}
=>x\(\in\){1;-3;3;-5;7;-9}
c)\(\frac{3x+7}{x-1}=\frac{3\left(x-1\right)+10}{x-1}=\frac{3\left(x-1\right)}{x-1}+\frac{10}{x-1}\in Z\)
=>10 chia hết x-1
=>x-1\(\in\)Ư(10)
bạn tự làm tiếp nhé
10 + (2x - 1) 2 : 3 = 13
=> (2x - 1) 2 : 3 = 13 - 10
=> (2x - 1) 2 : 3 = 3
=> (2x - 1) 2 = 3 . 3
=> (2x - 1) 2 = 3 2
=> 2x - 1 = 3
=> 2x = 3 + 1
=> 2x = 4
=> x = 2
10 + (2x - 1)2 : 3 = 13
=> (2x - 1)2 : 3 = 13 - 10
=> (2x - 1 )2 : 3 = 3
=> (2x - 1)2 = 9
=> (2x - 1)2 = 32
=> 2x - 1 = 3
=> 2x = 4
=> x = 2
Vậy x = 2
a) \(\left(x-3\right)\left(6-x\right)>0\)
\(\Rightarrow\)\(\hept{\begin{cases}x-3>0\\6-x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>3\\x< 6\end{cases}\Leftrightarrow}3< x< 6}\)
hoặc \(\hept{\begin{cases}x-3< 0\\6-x< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< 3\\x>6\end{cases}}}\)(vô lí)
Vậy \(3< x< 6\)
a, x-1 chia hết cho x+3
suy ra x+3-4 chia hết cho x+3
suy ra 4 chia hết cho x+3( do x+3 chia hết cho x+3)
suy ra x+3 thuộc ước của 4
hay x+3 thuộc 1;-1;2;-2;4;-4
x thuộc -2;-4;-1;-5;1;-7
vạy x thuộc -2;-4;-1;-5;1;-7 là nghiệm
a) x - 1 = x + 3 - 4
Để x - 1 chia hết cho x + 3 thì 4 phải chia hết cho x + 3
=> x + 3 \(\in\) Ư(4) = {-4;-2;-1;1;2;4}
Nếu x + 3 = -4 => x = -7
Nếu x + 3 = -2 => x = -5
Nếu x + 3 = -1 => x = -4
Nếu x + 3 = 1 => x = -2
Nếu x + 3 = 2 => x = -1
Nếu x + 3 = 4 => x = 1
Vậy x \(\in\) {-7;-5;-4;-2;-1;1}
b) 2x = 2x - 2 + 2 = 2(x - 1) + 2
Để 2x chia hết cho x - 1 thì 2 phải chia hết cho x - 1
=> x - 1 \(\in\) Ư(2) = {-2;-1;1;2}
Nếu x - 1 = -2 => x = -1
Nếu x - 1 = -1 => x = 0
Nếu x - 1 = 1 => x = 2
Nếu x - 1 = 2 => x = 3
Vậy x \(\in\) {-1;0;2;3}
a)\(x-15\%x=\frac{1}{3}\)
\(x.\left(1-15\%\right)=\frac{1}{3}\)
\(x.\frac{-280}{3}=\frac{1}{3}\)
\(x=\frac{1}{3}:\frac{-280}{3}\)
\(x=\frac{-1}{280}\)
Vậy \(x=\frac{-1}{280}\)
b)\(\frac{4}{5}x-x-\frac{3}{2}x+\frac{6}{5}=\frac{1}{2}-\frac{4}{3}\)
\(-\frac{17}{10}x+\frac{6}{5}=\frac{-5}{6}\)
\(-\frac{17}{10}x=-\frac{5}{6}-\frac{6}{5}\)
\(-\frac{17}{10}x=\frac{-61}{30}\)
\(x=\frac{-61}{30}:\frac{-17}{10}\)
\(x=\frac{61}{51}\)
Vậy \(x=\frac{61}{51}\)
a) Ta có: \(\left|2x-\dfrac{1}{3}\right|\ge0\forall x\)
\(\Leftrightarrow\left|2x-\dfrac{1}{3}\right|-\dfrac{7}{4}\ge-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi \(2x=\dfrac{1}{3}\)
hay \(x=\dfrac{1}{6}\)
Vậy: \(A_{min}=-\dfrac{7}{4}\) khi \(x=\dfrac{1}{6}\)
b) Ta có: \(\dfrac{1}{3}\left|x-2\right|\ge0\forall x\)
\(\left|3-\dfrac{1}{2}y\right|\ge0\forall y\)
Do đó: \(\dfrac{1}{3}\left|x-2\right|+\left|3-\dfrac{1}{2}y\right|\ge0\forall x,y\)
\(\Leftrightarrow\dfrac{1}{3}\left|x-2\right|+\left|3-\dfrac{1}{2}y\right|+4\ge4\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2=0\\3-\dfrac{1}{2}y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=6\end{matrix}\right.\)
Vậy: \(B_{min}=4\) khi x=2 và y=6
