Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Dòng điện sớm pha hơn điện áp -> Zc> Z L .
Khi R=Ro công suất tiêu thụ của mạch là cực đại, ta có
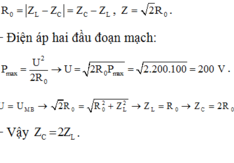

Chọn B
Dòng điện sơm pha hơn điện áp ![]()
Khi R = R 0 công suất tiêu thụ cảu mạch là cực đại, ta có
![]()
![]()
Điện áp hai đầu đoạn mạch
![]()
![]()
![]()

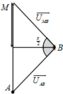
Đồ thị biểu diễn mỗi liên hệ giữa uMB và uAB có dạng là đường tròn
→ u A B ⊥ u M B U A B = U M B
Biểu diễn vecto các điện áp.
→Dễ thấy MBA vuông cân tại B
→ R = 0 , 5 Z L = 100 Ω
→ Đáp án A

\(u_{AN}=u_C+u_R=200\cos(100\pi t+\dfrac{\pi}{6})\)(1)
\(u_{MB}=u_R+u_L=200\cos(100\pi t+\dfrac{\pi}{3})\)(2)
Biểu diễn bằng giản đồ véc tơ ta có:
O U U U U U AN MB R L C 15 0
Từ giản đồ ta thấy: Hiệu điện thế 2 đầu mạch là: \(u=u_R\)
\(U_{0R}=U_{0MB}.\cos 15^0=200.\cos15^0=193V\)
\(\varphi_R=\dfrac{\pi}{3}-\dfrac{\pi}{12}=\dfrac{\pi}{4}\)
\(\Rightarrow u=u_R=193.\cos(100\pi t+\dfrac{\pi}{4})V\)
Hình như là k đúng lắm ạ? Bởi vì trong đáp án k có kết quả đấy ạ!
Bài này vẽ giản đồ véc tơ sẽ ra được thôi bạn.
O U U U U U 0AN 0R oMB 0L 0C α α
Ta có: \(\dfrac{1}{U_{0R}^2}=\dfrac{1}{U_{0AN}^2}+\dfrac{1}{U_{0MB}^2}\)
\(\Rightarrow U_{0R}=50\sqrt 3(cm)\)
\(\Rightarrow U_{0L}=\sqrt{(100\sqrt 3)^2-(50\sqrt 3)^2}=150V\)
\(\tan\alpha=\dfrac{U_{0AN}}{U_{0MB}}=\dfrac{1}{\sqrt 3}\Rightarrow \alpha=\pi/6\)
\(\Rightarrow \varphi_L=\varphi_{MB}+\pi/6=\pi/6\)
\(\Rightarrow u_L=150\cos(100\pi t +\dfrac{\pi}{6})\)(V)
Vậy: \(u_{AB}=u_{AN}+u_L\)
Dùng máy tính tổng hợp 2 dao động \(u_{AN}\) và \(u_L\) ta được \(u_{AB}\)
Bạn tính tiếp nhé.
làm sao nhỉ