Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
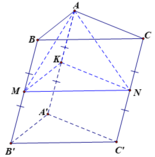
Gọi K là trung điểm của AA' và V, VABC.KMN, VA.KMN lần lượt là thể tích khối lăng trụ ABC. A'B'C' khối lăng trụ ABC. KMN và thể tích khối chóp A. MNK. Khi đó
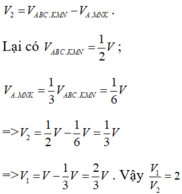

Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk

4.
Qua G kẻ đường thẳng song song AB lần lượt cắt AC và BC tại M và N
\(\Rightarrow A'B'NM\) là thiết diện của (A'B'G) và lăng trụ
Theo Talet ta có \(\frac{CM}{AC}=\frac{CN}{BC}=\frac{2}{3}\Rightarrow CM=CN=\frac{2a}{3}\)
Kéo dài A'M, B'N, C'C đồng quy tại P (theo tính chất giao tuyến 3 mặt phẳng)
Do \(CN//B'C'\Rightarrow\frac{PC}{PC'}=\frac{CN}{B'C'}=\frac{2}{3}\Rightarrow\frac{PC}{PC+CC'}=\frac{2}{3}\)
\(\Rightarrow3PC=2\left(PC+a\right)\Rightarrow PC=2a\)
\(\Rightarrow PC'=3a\)
\(MN=\frac{2}{3}BC\Rightarrow S_{CMN}=\frac{4}{9}S_{ABC}=\frac{4}{9}.\frac{a^2\sqrt{3}}{4}=\frac{a^2\sqrt{3}}{9}\)
\(V_{P.A'B'C'}=\frac{1}{3}PC'.S_{A'B'C'}=\frac{1}{3}.3a.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{4}\)
\(V_{P.CMN}=\frac{1}{3}PC.S_{CMN}=\frac{1}{3}.2a.\frac{a^2\sqrt{3}}{9}=\frac{2a^3\sqrt{3}}{27}\)
\(\Rightarrow V_{CMN.A'B'C'}=\frac{a^3\sqrt{3}}{4}-\frac{2a^3\sqrt{3}}{27}=\frac{19a^3\sqrt{3}}{108}\)
\(\Rightarrow V_{MNABA'B'}=\frac{a^3\sqrt{3}}{4}-\frac{19a^3\sqrt{3}}{108}=\frac{2a^3\sqrt{3}}{27}\)
2.
Đề thiếu dữ kiện ko tính được, chỉ tính được trong trường hợp tam giác ABC là vuông cân.
3.
\(AC=BC=a\sqrt{2}\) ; \(AC=AB\sqrt{2}=2a\)
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\Rightarrow BM\perp\left(ACC'A'\right)\)
\(\Rightarrow\widehat{BA'M}\) là góc giữa A'B và (ACC'A')
\(\Rightarrow\widehat{BA'M}=30^0\)
\(BM=\frac{1}{2}AC=a\)
\(tan\widehat{BA'M}=\frac{BM}{A'M}\Rightarrow A'M=\frac{BM}{tan30^0}=a\sqrt{3}\)
\(A'A=\sqrt{A'M^2-AM^2}=a\sqrt{2}\)
\(V=\frac{1}{2}A'A.AB.BC=a^3\sqrt{2}\)
Ko đáp án nào đúng

Chọn B
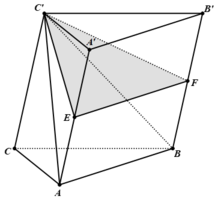
Gọi E, F lần lượt là các trung điểm của AA' và BB' khi đó ta có:
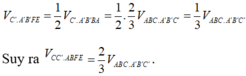
Vậy mặt phẳng (C'EF) chia khối lăng trụ thành hai phần có tỉ số thể tích bằng 1 2 .

5.
Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\)
\(\Rightarrow BC\perp\left(A'AM\right)\)
\(\Rightarrow\widehat{A'MA}\) là góc giữa (A'BC) và (ABC)
\(\Rightarrow\widehat{A'MA}=60^0\)
\(AM=\frac{a\sqrt{3}}{2}\Rightarrow A'A=AM.tan60^0=\frac{3a}{2}\)
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=B.A'A=\frac{3\sqrt{3}}{8}a^3\)
1.
\(V=Bh\)
2.
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=Bh=\frac{a^2\sqrt{3}}{4}.a\sqrt{6}=\frac{3\sqrt{2}}{4}a^3\)
3.
\(B=\frac{1}{2}\left(a\sqrt{2}\right)^2=a^2\Rightarrow V=Bh=a^2.5a=5a^3\)
4.
\(h=\sqrt{\left(2a\right)^2-\left(a\sqrt{3}\right)^2}=a\)
\(B=\frac{\left(a\sqrt{3}\right)^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{4}a^2\)
\(V=Bh=\frac{3\sqrt{3}}{4}a^3\)
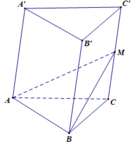
Đáp án C
Hình chóp MABC có cùng diện tích đáy với hình lăng trụ
Và có chiều cao bằng 1 2 lăng trụ nên
V 2 = 1 6 V A B C . A ' B ' C ' ⇒ V 1 = 5 6 V A B C . A ' B ' C '
⇒ V 1 V 2 = 5