Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số quân lính vận chuyển ngựa sắt là:
\(1250+2320=3570\left(quân\right)\)
Số quân lính để vận chuyện ngựa, gươm, áo giáp và nón sắt đến cho tráng sĩ là:
\(1250+3570=4820\left(quân\right)\)

Câu 1.
a) Gọi O=AC∩BD⇒SO⊥(ABCD).O=AC∩BD⇒SO⊥(ABCD).
Ta có ABCD là hình vuông cạnh a nên AC=BD=a2–√⇒AO=a2√2.AC=BD=a2⇒AO=a22.
Xét tam giác vuông SOA có: SO=SA2−OA2−−−−−−−−−√=2a2−a22−−−−−−−√=a6√2.SO=SA2−OA2=2a2−a22=a62.
SABCD=a2⇒VS.ABCD=13SO.SABCD=13a6–√2.a2=a36–√6.SABCD=a2⇒VS.ABCD=13SO.SABCD=13a62.a2=a366.
Gọi A’ là trung điểm của SA.
Trong (SAC) qua A’ kẻ đường thẳng vuông góc với SA cắt SO tại I.
Suy ra I là tâm mặt cầu ngoại tiếp chóp S.ABCD.
Dễ thấy
ΔSA′I đồng dạng ΔSOA(g.g)⇒SASI=SOSA′⇒SI=SA.SA′SO=a2–√.a2√2a6√2=a6–√3=RΔSA′I đồng dạng ΔSOA(g.g)⇒SASI=SOSA′⇒SI=SA.SA′SO=a2.a22a62=a63=R
Ta có A’C’ // (ABCD) ⇒d(A′;(ABCD))=d(C′;(ABCD))⇒d(A′;(ABCD))=d(C′;(ABCD))
⇒VA′.ABCD=VC′.CBAD.⇒VA′.ABCD=VC′.CBAD.
Vậy hai khối chóp A’.ABCD và C’.CBAD bằng nhau.

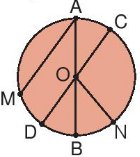
a) Đường kính: DC, AB
Bán kính: OA, OB, OC, OD, ON
b) Hình dưới đây được xếp bởi 16 khối lập phương, 3 khối trụ

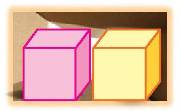
a) Vì trong hộp có khối lập phương màu vàng nên khả năng lấy được khối lập phương màu vàng là Có thể.
Có thể lấy được khối lập phương màu vàng.
b) Vì trong hộp có khối lập phương màu hồng nên khả năng lấy được khối lập phương màu hồng là Có thể.
Có thể lấy được khối lập phương màu hồng.
c) Vì trong hộp không có khối lập phương màu đỏ nên khả năng lấy được khối lập phương màu đỏ là Không thể.
Không thể lấy được khối lập phương màu đỏ.

Giải:
a; Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số áo của khối 5 là:
1020: (3+ 2) x 2 = 408(cái áo)
Số áo khối 4 đã mua là:
1020 - 408 = 612(cái áo)
b; Khối 4 đã quyên góp vào quỹ từ thiện là:
50 000 x 612 = 30 600 000 (đồng)
Đáp số: a; Khối 4 mua 612 cái áo
Khối 5 đã mua 408 cái áo
b; Khối 4 đã quyên góp 30 600 000 (đồng)

Lời giải:
a. Tổng số phần bằng nhau: $3+2=5$ (phần)
Số áo khối 4: $1020:5\times 3=612$ (chiếc)
Số áo khô 5: $1020:5\times 2=408$ (chiếc)
b. Học sinh khối 4 đã ủng hộ được số tiền là:
$1020\times 50000=51000000$ (đồng)

a, Khối 3 và 5 có :
126:2 = 63 ( học sinh )
b, Khối 4 có 126 x 2 = 252 ( học sinh )
c, Khối 4 hơn khối 3 và 5 : 252-63= 189 ( học sinh )



Thể tích khối nón là:
\(V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi a^2.2a=\dfrac{2\pi a^3}{3}\)