K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

29 tháng 3 2016
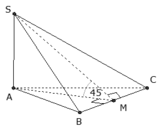
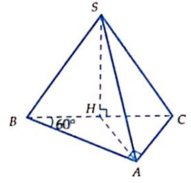
Gọi H là trung điểm của BC, suy ra \(SH\perp BC\). Mà (SBC) vuông góc với (ABC) theo giao tuyến BC, nên \(SH\perp\left(ABC\right)\)
Ta có : \(BC=a\Rightarrow SH=\frac{a\sqrt{3}}{2}\); \(AC=BC\sin30^0=\frac{a}{2}\)
\(AB=BC.\cos30^0=\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABC}=\frac{1}{6}SH.AB.AC=\frac{a^3}{16}\)
Tam giác ABC vuông tại A và H là trung điểm của BC nên \(HA=HB\). Mà \(SH\perp\left(ABC\right)\), suy ra \(SA=SB=a\). Gọi I là trung điểm của AB, suy ra \(SI\perp AB\)
Do đó \(SI=\sqrt{SB^2-\frac{AB^2}{4}}=\frac{a\sqrt{13}}{4}\)
Suy ra \(d\left(C;\left(SAB\right)\right)=\frac{3V_{S.ABC}}{S_{SAB}}=\frac{6V_{S.ABC}}{SI.AB}=\frac{a\sqrt{39}}{13}\)
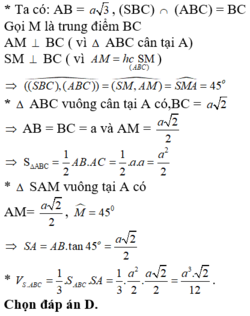

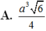
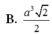
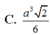
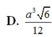

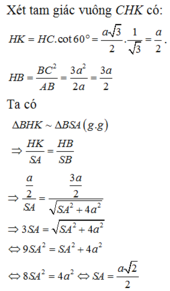
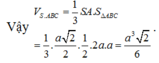
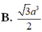
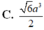
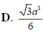
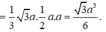



Chọn D
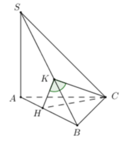
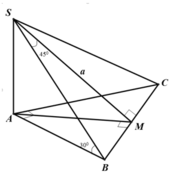
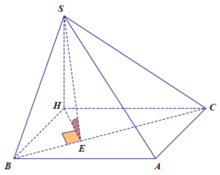
Từ C kẻ CH ⊥ AB tại H. Từ H kẻ HK ⊥ SB tại K.
+ Giao tuyến của hai mặt phẳng (SBC) và (SAB) là SB.
mà CK ∈ (SBC)
Do đó góc giữa hai mặt phẳng (SBC) và (SAB) là C K H ^ = 30 O
Tam giác SBC vuông tại C có góc B S C ^ = 60 O nên
+ Tam giác SBC vuông tại C có CK là đường cao nên
+ Tam giác CKH vuông tại H (vì CH ⊥ (SAB)) và C K H ^ = 30 O có nên
+ Tam giác ABC vuông tại C và có CH là đường cao nên
+ Tam giác ABC vuông tại C nên
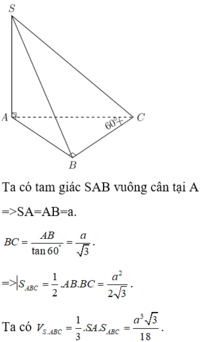
+ Tam giác SAB vuông tại nên A
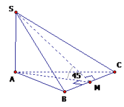
Thể tích khối chóp là