Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng 5 chữ số bất kì luôn \(\ge0+1+2+3+4=10\) => Mọi chữ số đề \(\le8\)
Nếu X không có 0 tổng 5 chữ số bất kì luôn \(\ge1+2+3+4+5=15\) => Mọi chữ số đều \(\le3\) ---> Vô lý
Vậy X luôn có 0 và không có 9.
Các X bộ số thỏa mãn:
+) \(\left(0;1;2;3;4;8\right)\) lập được 5.5! = 600 số tự nhiên và 5! + 3.4.4! = 408 số chẵn
+) \(\left(0;1;2;3;5;7\right)\) lập được 5.5! = 600 số tự nhiên và 5! + 4.4! = 216 số chẵn
+) \(\left(0;1;2;4;5;6\right)\) lập được 5.5! = 600 số tự nhiên và 5! + 3.4.4! = 408 số chẵn
=> Xác suất chọn được số chẵn: \(P=\dfrac{408+408+216}{600\cdot3}=\dfrac{43}{75}\)

Gọi số đó là \(\overline{abcdef}\Rightarrow a+b+c+d+e+f=1+2+3+4+5+6=21\)
Mặt khác \(a+b+c=d+e+f-1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=10\\d+e+f=11\end{matrix}\right.\)
\(\Rightarrow\left(a;b;c\right)=\left(1;3;6\right);\left(1;4;5\right);\left(2;3;5\right)\)
Số số thỏa mãn: \(3.\left(3!.3!\right)=108\)
Xác suất: \(P=\dfrac{108}{6!}=\dfrac{3}{20}\)

n(S)=6!
Để thỏa mãn yêu cầu đề bài thì cần chọn ra 3 số có tổng là 12
=>Số trường hợp thỏa mãn là (1;5;6); (2;4;6); (3;4;5)
=>Có 3*3!*3!
=>P=3/20

Đáp án A.
Gọi số cần tìm có dạng a b c d vì chia hết cho 6
⇒ d = { 2 , 4 , 6 , 8 } a + b + c + d : 3
Khi đó, chọn d có 4 cách chọn, b và c đều có 9 cách chọn (từ 1 → 9).
+) Nếu a + b + c + d : 3 thì a = {3,6,9} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 1 thì a = {2,5,8} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 2 thì a = {1,4,7} => có 3 cách chọn a.
Suy ra a chỉ có 3 cách chọn => có 4.9.9.3 = 972 số chia hết cho 6.
Vậy xác suất cần tính là P = 972 9 4 = 4 27 .

Có 900 số tự nhiên có 3 chữ số \( \Rightarrow n\left( \Omega \right) = 900\)
Gọi \({A_1}\) là biến cố: “Số được chọn chia hết cho 2”, \({A_2}\) là biến cố “Số được chọn chia hết cho 7”.
Vậy \({A_1}{A_2}\) là biến cố “Số được chọn chia hết cho 14”, \(A = {A_1} \cup {A_2}\) là biến cố “Số được chọn chia hết cho 2 hoặc 7”.
Có 450 số có 3 chữ số chia hết cho 2 \( \Rightarrow n\left( {{A_1}} \right) = 450 \Rightarrow P\left( {{A_1}} \right) = \frac{{n\left( {{A_1}} \right)}}{{n\left( \Xi \right)}} = \frac{{450}}{{900}} = \frac{1}{2}\)
Có 128 số có 3 chữ số chia hết cho 7 \( \Rightarrow n\left( {{A_2}} \right) = 128 \Rightarrow P\left( {{A_2}} \right) = \frac{{n\left( {{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{128}}{{900}} = \frac{{32}}{{225}}\)
Có 64 số có 3 chữ số chia hết cho 14
\( \Rightarrow n\left( {{A_1}{A_2}} \right) = 64 \Rightarrow P\left( {{A_1}{A_2}} \right) = \frac{{n\left( {{A_1}{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{64}}{{900}} = \frac{{16}}{{225}}\)
\( \Rightarrow P\left( A \right) = P\left( {{A_1} \cup {A_2}} \right) = P\left( {{A_1}} \right) + P\left( {{A_2}} \right) - P\left( {{A_1}{A_2}} \right) = \frac{1}{2} + \frac{{32}}{{225}} - \frac{{16}}{{225}} = \frac{{257}}{{450}}\)
Gọi \({B_1}\) là biến cố: “Số được chọn có 3 chữ số chẵn”, \({B_2}\) là biến cố “Số được chọn có 1 chữ số chẵn và 2 chữ số lẻ”.
Vậy \(B = {B_1} \cup {B_2}\) là biến cố “Số được chọn có tổng các chữ số là số chẵn”.
Có \(4.5.5 = 100\) số có 3 chữ số chẵn \( \Rightarrow n\left( {{B_1}} \right) = 100 \Rightarrow P\left( {{B_1}} \right) = \frac{{n\left( {{B_1}} \right)}}{{n\left( \Omega \right)}} = \frac{{100}}{{900}} = \frac{1}{9}\)
Có \(4.5.5 = 100\) số có 3 chữ số có chữ số hàng trăm chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng chục chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng đơn vị chẵn, 2 chữ số còn lại lẻ.
\( \Rightarrow n\left( {{B_2}} \right) = 100 + 125 + 125 = 350 \Rightarrow P\left( {{B_2}} \right) = \frac{{n\left( {{B_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{350}}{{900}} = \frac{7}{{18}}\)
Vì \({B_1}\) và \({B_2}\) là hai biến cố xung khắc nên ta có:
\(P\left( B \right) = P\left( {{B_1} \cup {B_2}} \right) = P\left( {{B_1}} \right) + P\left( {{B_2}} \right) = \frac{1}{9} + \frac{7}{{18}} = \frac{1}{2}\)

Đáp án B.
Số phần tử của E là ![]() .
.
Từ 5 chữ số đã cho ta có 4 bộ gồm 3 chữ số có tổng chia hết cho 3 là ![]() . Mỗi bộ 3 chữ số này ta lập được
. Mỗi bộ 3 chữ số này ta lập được ![]() số thuộc tập hợp E. Vậy trong tập hợp E có
số thuộc tập hợp E. Vậy trong tập hợp E có ![]() số chia hết cho 3.
số chia hết cho 3.
Gọi A là biến cố “Số được chọn từ E chia hết cho 3” thì ![]() .
.
Vậy xác suất cần tính là 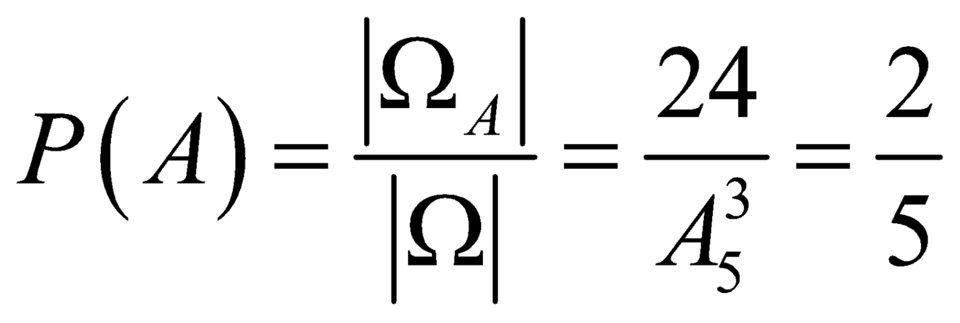 .
.




Ta có: \(\left|K\right|=9.10^3=9000\)
Gọi A là tập hợp các số tự nhiên có 4 chữ số mà tổng các chữ số của nó chia hết cho 4.
\(A=\left\{\overline{abcd}\inℕ:\left(a+b+c+d\right)⋮4\right\}\)
Xét \(b+c+d=4k+r\left(0\le r\le3\right)\)
Nếu \(r\in\left\{0;1;2\right\}\) thì mỗi giá trị của r sẽ có 2 giá trị của a sao cho \(\left(a+b+c+d\right)⋮4\)( đó là a=4-r, a=8-r)
Nếu \(r=3\) thì mỗi giá trị của r sẽ có 3 giá trị của a sao cho \(\left(a+b+c+d\right)⋮4\) ( đó là a=1, a=5, a=9)
Gọi \(B=\left\{\overline{bcd}\inℕ:0\le b,c,d\le9;b+c+d=4k+r;0\le r\le2\right\}\)
\(C=\left\{\overline{bcd}\inℕ:0\le b,c,d\le9;b+c+d=4k+3\right\}\)
Khi đó ta có: \(\left|A\right|=2 \left|B\right|+3\left|C\right|=2\left(\left|B\right|+\left|C\right|\right)+\left|C\right|=2.10^3+\left|C\right|\)
Xét tập hợp C với c+d =4m+n .
Nếu \(n\in\left\{0;1\right\}\) thì mỗi giá trị của n sẽ có 2 giá trị của b sao cho b+c+d=4k+3
Nếu \(n\in\left\{2;3\right\}\) thì mỗi giá trị của n sẽ có 3 giá trị của b sao cho b+c+d=4k+3
Gọi \(D=\left\{\overline{cd}\inℕ:0\le c,d\le9;c+d=4m+n;0\le n\le1\right\}\)
\(E=\left\{\overline{c\text{d}}\inℕ:0\le c,d\le9;c+d=4m+n;2\le n\le3\right\}\)
Khi đó ta có: \(\left|C\right|=2\left|D\right|+3\left|E\right|=2\left(\left|D\right|+\left|E\right|\right)+\left|E\right|=2.10^2+\left|E\right|\), với \(\left|E\right|=25+24=49\)
\(\Rightarrow\left|A\right|=2.10^3+2.10^2+49=2249\)
Gọi biến cố X : '' Số được chọn có tổng các chữ số là bội của 4''. Khi đó xác suất của biến cố là : \(P\left(X\right)=\frac{2249}{9000}\)