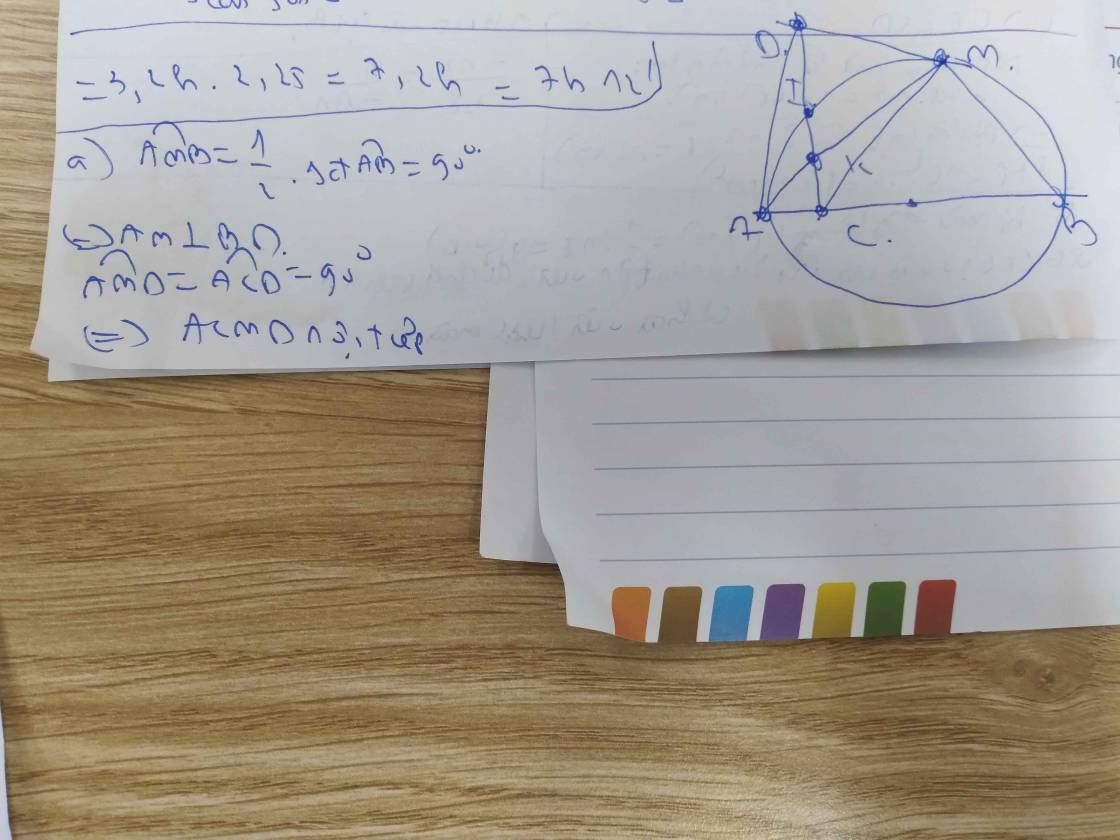
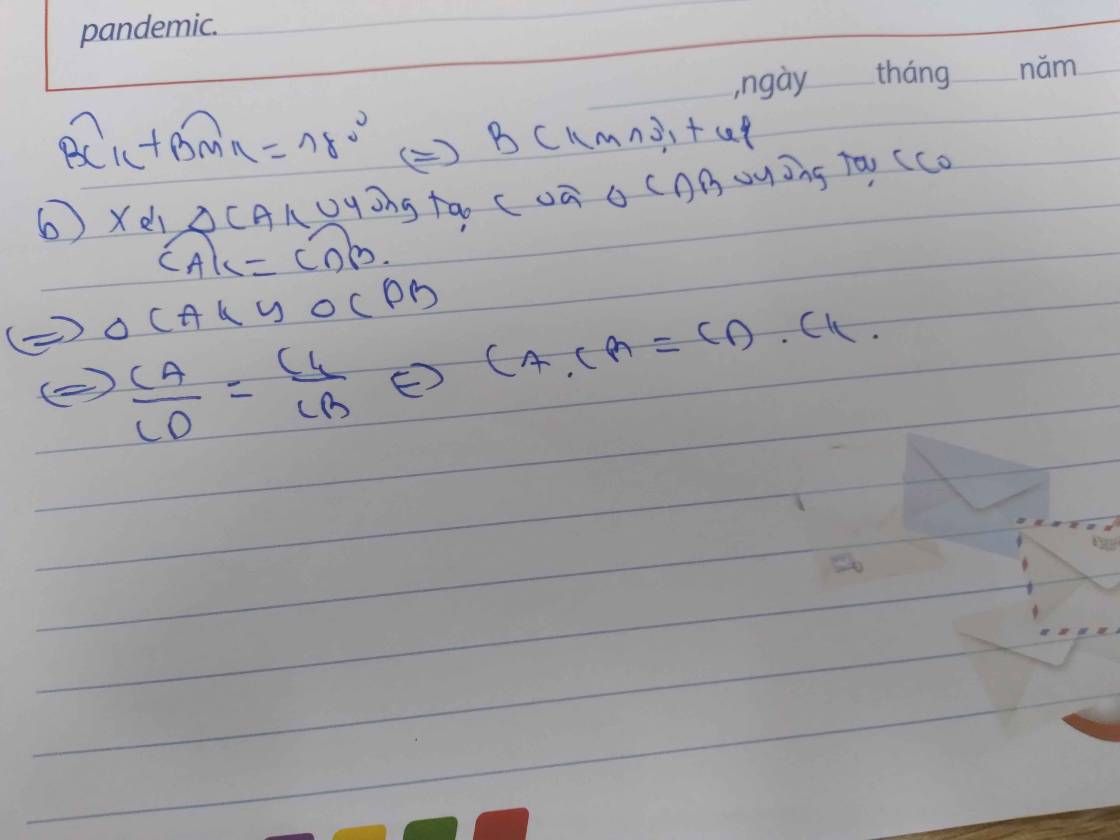Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D C B A 1 E M 1 P I F 1
Trên tia đối tia AB lấy P sao cho AP = BE
\(\Delta PAD=\Delta EBA\left(c.g.c\right)\)\(\Rightarrow\widehat{PDA}=\widehat{A_1}\)
Mà \(\widehat{D_1}=\widehat{E_1}\)( c/m )
Ta có : \(\widehat{PDE}+\widehat{DEF}=\widehat{PDA}+\widehat{D_1}+\widehat{FED}=\widehat{A_1}+\widehat{E_1}+\widehat{FED}=90^o\)
\(\Rightarrow EF\perp PD\)
Xét \(\Delta PBC\)và \(\Delta ECD\)có :
PB = EC ; \(\widehat{PBC}=\widehat{ECD}\); BC = CD
\(\Rightarrow\Delta PBC=\Delta ECD\left(c.g.c\right)\)
\(\Rightarrow\widehat{CPB}=\widehat{E_1}\)
Ta có : \(\widehat{CPB}+\widehat{PID}=\widehat{E_1}+\widehat{EIB}=90^o\)
\(\Rightarrow CP\perp ED\)
do đó : F là trực tâm \(\Delta EPD\)
\(\Rightarrow DF\perp EP\) ( 1 )
Xét \(\Delta EPC\)có : \(PB\perp EC;EI\perp CP\) nên I là trực tâm \(\Delta EPC\)
\(\Rightarrow CM\perp EP\) ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow DF//IM\Rightarrow\frac{MI}{FD}=\frac{EI}{ED}=\frac{EM}{EF}\) ( 3 )
\(IB//CD\Rightarrow\frac{EB}{EC}=\frac{EI}{ED}\) ( 4 )
Từ ( 3 ) và ( 4 ) suy ra \(\frac{MI}{FD}=\frac{EB}{EC}\Rightarrow BM//FC\)
\(\Rightarrow BM\perp DE\)
p/s : mệt

a: Xét tứ giác BMKC có \(\widehat{BMK}+\widehat{KCB}=180^0\)
nên BMKC là tứ giác nội tiếp
b: Xét ΔBMA vuông tại M và ΔBCD vuông tại C có
góc B chung
Do đó: ΔBMA\(\sim\)ΔBCD
Suy ra: BM/BC=BA/BD
hay BM/BA=BC/BD
=>ΔBMC\(\sim\)ΔBAD
nên \(\widehat{BMC}=\widehat{BAD}\)

1:
Xét (O) có
góc CAN=1/2*sđ cung CN
góc BAN=1/2*sđ cung NB
mà sđ cung CN=sđ cung NB
nên góc CAN=góc BAN
=>AN là phân giác của góc CAB
Xet (O) có
góc CBM=1/2*sd cung CM
góc ABM=1/2*sđ cung AM
mà sđ cung CM=sđ cung AM
nên góc CBM=góc ABM
=>BM là phân giác của góc CBA
Xét ΔCAB có
AI,BI là phân giác
=>I là tam đường tròn nội tiếp
=>CI là phân giác của góc ACB

1. Để chứng minh cung DE có số đo không đổi, ta cần chứng minh góc \(\angle BOC\) có số đo không đổi. Thực vậy, theo tính chất hai tiếp tuyến cắt nhau, OB và OC là phân giác ngoài của tam giác ABC. Ta có
\(\angle BOC=180^{\circ}-\frac{\angle MBC}{2}-\frac{\angle NCB}{2}=\frac{\angle ABC}{2}+\frac{\angle ACB}{2}=90^{\circ}-\frac{\angle BAC}{2}=90^{\circ}-\frac{a}{2}\)
Do đó góc \(\angle BOC\) có số đo không đổi. Suy ra cung DE có số đo không đổi.
2. Do CD vuông góc với AB nên BC,BD là đường kính của hai đường tròn (O) và (O'). Suy ra
\(\angle CFB=\angle DEB=90^{\circ}\to\angle CFD=\angle CED=90^{\circ}.\) Vậy tứ giác CDEF nội tiếp. Do đó \(\angle ECF=\angle EDF\to\angle FAB=\angle ECF=\angle EDF=\angle EDB\)
Vậy AB là phân giác của góc AEF.
3. Đề bài có chút nhầm lẫn, "kẻ \(IH\perp BC\) mới đúng. Do tam giác ABC nhọn và I nằm trong nên các điểm H,K,L nằm trên các cạnh của tam giác. Sử dụng bất đẳng thức \(a^2+b^2\ge\frac{1}{2}\left(a+b\right)^2,\) ta suy ra \(AL^2+BL^2\ge\frac{1}{2}\left(AL+BL\right)^2=\frac{1}{2}AB^2.\) Tương tự ta cũng có \(BH^2+CH^2\ge\frac{1}{2}BC^2,KC^2+KA^2\ge\frac{1}{2}AC^2.\) Mặt khác theo định lý Pitago
\(AL^2+BH^2+CK^2=\left(IA^2-IL^2\right)+\left(IB^2-IH^2\right)+\left(IC^2-IK^2\right)\)
\(=\left(IA^2-IK^2\right)+\left(IB^2-IL^2\right)+\left(IC^2-IH^2\right)\)
\(=BL^2+CH^2+AK^2.\)
Thành thử \(AL^2+BH^2+CK^2=\frac{\left(AL^2+BL^2\right)+\left(BH^2+CH^2\right)+\left(CK^2+AK^2\right)}{2}\ge\frac{AB^2+BC^2+CA^2}{2}.\)
Dấu bằng xảy ra khi \(AL=BL,BH=CH,CK=AK\Leftrightarrow I\) là giao điểm ba đường trung trực.