Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Sửa đề: AD=6cm
BC=AD=6cm
CD=AB=8cm
BD=căn 6^2+8^2=10cm
Xét ΔBCD vuông tại C có sin DBC=DC/BD=8/10=4/5
nên góc DBC=53 độ
=>góc BDC=37 độ
b: CH=6*8/10=4,8cm
BH=BC^2/BD=6^2/10=3,6cm

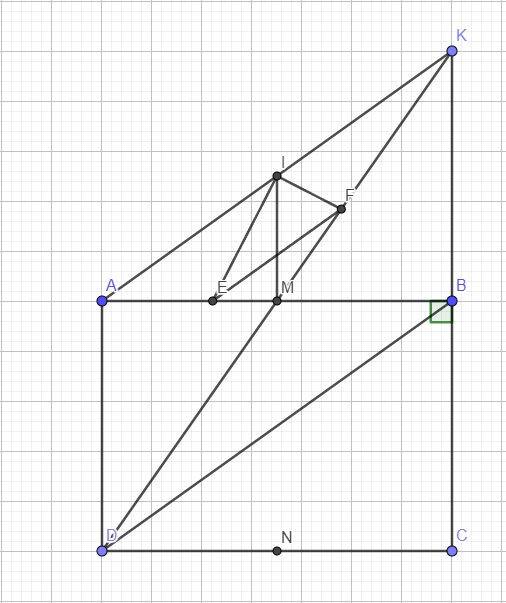
a: Xét tứ giác ADBK có
M là trung điểm chung của AB và DK
=>ADBK là hình bình hành
=>AK=DB
mà DB=AC(ABCD là hình chữ nhật)
nên AK=AC
=>ΔAKC cân tại A
b: Xét ΔIAM có IE là phân giác
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IA}\)
mà IA=IK
nên \(\dfrac{ME}{EA}=\dfrac{IM}{IK}\)
Xét ΔIMK có IF là phân giác
nên \(\dfrac{IM}{IK}=\dfrac{MF}{FK}\)
=>\(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
Xét ΔMAK có \(\dfrac{ME}{EA}=\dfrac{MF}{FK}\)
nên EF//AK
Ta có: EF//AK
AK//BD(AKBD là hình bình hành)
Do đó: EF//BD

a.
Xét tứ giác ADBK có: hai đường chéo AB và DK cắt nhau tại trung điểm M của mỗi đường
\(\Rightarrow ADBK\) là hình bình hành
Do ABCD là hình chữ nhật \(\Rightarrow AB\perp BC\Rightarrow AB\) là đường cao tam giác ACK
Theo cmt, ADBK là hbh \(\Rightarrow BK=AD\)
Mà \(AD=BC\) (ABCD là hcn)
\(\Rightarrow BK=BC\Rightarrow AB\) là trung tuyến tam giác ACK
\(\Rightarrow AB\) vừa là đường cao vừa là trung tuyến nên tam giác ACK cân tại A
b.
Do IE là phân giác, áp dụng định lý phân giác trong tam giác IAM:
\(\dfrac{EM}{EA}=\dfrac{IM}{IA}\) (1)
Do IF là phân giác, áp dụng định lý phân giác trong tam giác IMK:
\(\dfrac{FM}{FK}=\dfrac{IM}{IK}\) (2)
Mà I là trung điểm AK \(\Rightarrow IA=IK\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{EM}{EA}=\dfrac{FM}{FK}\Rightarrow EF||AK\) (định lý Talet đảo)
Theo c/m câu a do ADBK là hình bình hành \(\Rightarrow AK||BD\)
\(\Rightarrow EF||BD\)

Xét \(\Delta ABK\),ta có: BE là phân giác \(\angle ABK,BE\bot AK\)
\(\Rightarrow\Delta ABK\) cân tại B \(\Rightarrow BE\) là trung trực AK
Xét \(\Delta ABD\) và \(\Delta KBD:\) Ta có: \(\left\{{}\begin{matrix}AB=BK\\BDchung\\\angle ABD=\angle KBD\end{matrix}\right.\)
\(\Rightarrow\Delta ABD\sim\Delta KBD\left(c-g-c\right)\Rightarrow\angle BKD=\angle BAD=90\)
Ta có: \(\angle BAD+\angle BKD=90+90=180\Rightarrow BAKD\) nội tiếp
\(\Rightarrow\angle AKD=\angle ABD=\angle KBD=\angle KAH\left(=90-\angle BKA\right)\)
\(\Rightarrow\)\(AI\parallel KD\)
Vì \(I\in BE\Rightarrow IA=IK\Rightarrow\Delta IAK\) cân tại I \(\Rightarrow\angle IKA=\angle IAK\)
BADK nội tiếp \(\Rightarrow\angle KAD=\angle KBD=\angle ABD=\angle AKD\)
\(\Rightarrow\angle IKA=\angle DAK\Rightarrow\)\(IK\parallel AD\Rightarrow AIKD\) là hình bình hành
mà \(IA=IK\Rightarrow IKDA\) là hình thoi

a.
DO ABCD là hình vuông \(\Rightarrow\widehat{ACD}=45^0\)
\(\Rightarrow\widehat{ACD}=\widehat{EBN}\)
Mà \(\widehat{ACD}\) và \(\widehat{EBN}\) cùng chắn EN
\(\Rightarrow\) Tứ giác BENC nội tiếp
\(\Rightarrow\widehat{BEN}+\widehat{BCN}=180^0\)
\(\Rightarrow\widehat{BEN}=180^0-\widehat{BCN}=180^0-90^0=90^0\)
\(\Rightarrow NE\perp BM\) tại E
b.
Tương tự ta có tứ giác ABFM nội tiếp (\(\widehat{MAF}=\widehat{MBF}=45^0\) cùng chắn MF)
\(\Rightarrow\widehat{BFM}+\widehat{BAM}=180^0\)
\(\Rightarrow\widehat{BFM}=90^0\Rightarrow MF\perp BN\)
\(\Rightarrow I\) là trực tâm của tam giác BMN
\(\Rightarrow BI\perp MN\)
c.
Gọi H là giao điểm BI và MN
Do E và F cùng nhìn MN dưới 1 góc vuông
\(\Rightarrow\) Tứ giác EFMN nội tiếp
\(\Rightarrow\widehat{EMN}+\widehat{EFN}=180^0\)
Mà \(\widehat{EFN}+\widehat{EFB}=180^0\)
\(\Rightarrow\widehat{EMN}=\widehat{EFB}\)
Lại có tứ giác ABFM nội tiếp (A và F cùng nhìn BM dưới 1 góc vuông)
\(\Rightarrow\widehat{EFB}=\widehat{AMB}\) (cùng chắn AB)
\(\Rightarrow\widehat{EMN}=\widehat{AMB}\)
\(\Rightarrow\Delta_VAMB=\Delta_VHMB\left(ch-gn\right)\)
\(\Rightarrow AM=HM\)
Đồng thời suy ra \(AB=BH\Rightarrow BH=BC\) (do AB=BC)
Theo Pitago: \(\left\{{}\begin{matrix}HN=\sqrt{BN^2-BH^2}\\CN=\sqrt{BN^2-BC^2}\end{matrix}\right.\) \(\Rightarrow CN=HN\)
\(\Rightarrow AM+CN=MH+NH=MN\)
\(\Rightarrow MD+DN+MN=MD+DN+AM+CN=AD+CD=2a\)
Pitago: \(MN^2=DM^2+DN^2\ge\dfrac{1}{2}\left(DM+DN\right)^2\Rightarrow MN\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a-\left(DM+DN\right)\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a\ge\left(\dfrac{2+\sqrt{2}}{2}\right)\left(DM+DN\right)\ge\left(2+\sqrt{2}\right).\sqrt{DM.DN}\)
\(\Rightarrow DM.DN\le\left(6-4\sqrt{2}\right)a^2\)
\(\Rightarrow S_{MDN}=\dfrac{1}{2}DM.DN\le\left(3-2\sqrt{2}\right)a^2\)
Dấu "=" xảy ra khi \(DM=DN=\left(\sqrt{6}-\sqrt{2}\right)a\)
Xét tg vuông ADM và tg vuông DCN có
AM=DN (gt)
AD=CD (cạnh hình vuông)
=> tg ADM = tg DCN (hai tg vuông có 2 cạnh góc vuông bằng nhau) \(\Rightarrow\widehat{ADM}=\widehat{DCN}\)
b/
Ta có
BM=AB-AM
AN=AD-DN
AB=CD (cạnh hình vuông)
AM=DN (gt)
=> AN=BM (1)
AC=BD (đường chéo hình vuông) (2)
\(\widehat{CAN}=\widehat{BDM}=45^o\) (trong hình vuông đường chéo là đường phân giác của hai góc đối nhau) (3)
Từ (1) (2) (3) => tg ACN = tg BDM (c.g.c)
\(\Rightarrow\widehat{ACN}=\widehat{BDM}\) => CDIO là tứ giác nội tiếp
\(\Rightarrow\widehat{OIC}=\widehat{BDC}=45^o\) (góc nội tiếp cùng chắn cung OC) (4)
Ta có
\(\widehat{ADM}=\widehat{DCN}\) (cmt)
Xét tg vuông CDN có
\(\widehat{DCN}+\widehat{DNC}=90^o\Rightarrow\widehat{ADM}+\widehat{DNC}=90^o\Rightarrow\widehat{DIN}=90^o\)
\(\Rightarrow\widehat{MIC}=90^o\) (5)
Từ (4) và (5) \(\Rightarrow\widehat{OIM}=45^o\) (6)
Từ (4) và (6) \(\Rightarrow\widehat{OIC}=\widehat{OIM}=45^o\) => OI là phân giác của \(\widehat{MIC}\))