Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn tựu vẽ hk nha
a, dễ cm tứ giác ABCD là hình thang
ta có AD//MO//CB(cùng vuông góc vs DC)
A0=B0
từ đây suy ra DM=MC
B, TỪ M KẺ MH VUÔNG GÓC VS AB
TA CÓ GÓC DAM=GÓC AMO( do AD//MO) (1)
LẠI CÓ GÓC AMO=GÓC MAO( do MO=AO) (2)
TỪ (1)(2) SUY RA GÓC DAM=GÓC MAO
LẠI CÓ GÓC D=GÓC MHA=90
SUY RA TAM GIAC DMA=TAM GIAC HMA
SUY RA AD=AH
tự BC=HB
TỪ ĐÂY SUY RA AD+CB=AH+BH=AB KO ĐỔI
C, TA CÓ MH=DM=MC(CMT)
LẠI CÓ MHVUOONG GÓC VS AB
SUY RA DƯỜNG TRÒN CD TX VS AB
D, TRONG HT VUÔNG ABCD CÓ DC<=AB
SUY RA SABCD=\(\frac{\left(AD+CB\right).DC}{2}=\frac{AB.CD}{2}< =\frac{AB^2}{2}\)
DẤU = XẢY RA KHI M NẰM CHÍNH GIỬA CUNG AB

1. Ta có AD // OM // BC ; OA = OB
=> OM là đường trung bình của hình thang ABCD => M là trung điểm CD => MC = MD
2. Vì OM là đường trung bình của hình thang ABCD nên : \(OM=\frac{AD+BC}{2}\Rightarrow AD+BC=2OM\)không đổi.
3. Dễ thấy M là tâm của đường tròn đường kính CD vì MC = MD
Lại có AD vuông góc với MD => đpcm
4. Ta có : \(S_{ABCD}=\frac{1}{2}.\left(AD+BC\right).CD=OM.CD\)
Vì OM không đổi nên S.ABCD lớn nhất <=> CD lớn nhất <=> CD = AB
Vậy max (S.ABCD) = OM . AB = R.(2R) = 2R2 với R = AB/2

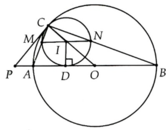
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm

Nhận xét: Tứ giác ABCD nội tiếp đường tròn đường kính AC vì ^ABC=^CDA=900. Gọi tâm của đường tròn này là O. Khi đó thì O chính là trung điểm đoạn AC. Ta thấy M là 1 điểm chung của (S) và (T), đồng thời là trung điểm BD nên M nằm trên trung trực BD. Gọi giao điểm thứ hai của (S) và (T) là L. Ta đi chứng minh L cũng nằm trên trung trực BD. Thật vậy:
Từ M kẻ MK vuông góc với đường thẳng ST. Gọi E,F lần lượt là hình chiếu của S,T lên MA,MC.
Khi đó các tứ giác KSEM, KTMS nội tiếp => ^EKF = ^MKE + ^MKF = ^MSE + ^MTF = (^ASM + ^CTM)/2
Ta thấy AC là tiếp tuyến chung của (S) và (T) nên ^MAC = ^ASM/2; ^MCA = ^CTM/2
Từ đó: ^EKF = ^MCA + ^MAC = ^EOA + ^FOC (Chú ý tứ giác MEOF là hbh) = 1800 - ^EOF
Suy ra tứ giác KEOF nội tiếp => ^EKO = ^EFO = ^MAC = ^MSE (=^ASM/2) = ^EKM
Mà M và O nằm cùng phía so với EK nên tia KM,KO trùng nhau hay O,M,K thẳng hàng
Mặt khác: (S) và (T) cắt nhau tại M và L nên ML vuông góc ST. Do MK vuông góc ST nên M,K,L thẳng hàng
Vì vậy 4 điểm O,M,K,L thẳng hàng. Lại có OM là trung trực của BD => ML cũng là trung trực BD
Hay 2 giao điểm của (S) và (T) cùng nằm trên đường trung trực của BD (đpcm).
có bt bùi diệu linh không lớp 6 nó thik cậu đó
hảo hán