Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Ta thấy \(\widehat{EAF}=\widehat{ECF}=90^o\Rightarrow\) C, A thuộc đường tròn đường kính EF hay E, A, C, F cùng thuộc đường tròn đường kính EF.
b. Do E, A, C, F cùng thuộc một đường tròn nên \(\widehat{CEF}=\widehat{CAF}=45^o\) (Góc nội tiếp cùng chắn một cung)
Lại có \(\widehat{ECF}=90^o\Rightarrow\) \(\Delta ECF\) vuông cân tại C hay CE = CF.
Do BC // DE nên \(\widehat{NCB}=\widehat{CED}\Rightarrow\Delta NBC\sim\Delta CDE\left(g-g\right)\)
\(\Rightarrow\frac{NB}{CD}=\frac{BC}{DE}\Rightarrow BN.DE=CD.BC=a^2\) không đổi.
c. Ta thấy BCFM là tứ giác nội tiếp nên \(\widehat{BCM}+\widehat{CMB}=\widehat{BFM}+\widehat{CFB}=\widehat{MFC}=45^o\)
Gọi tia đối của tia BM là Bx, ta có \(\widehat{CBx}=45^o;\widehat{CBD}=45^o\Rightarrow\)D thuộc tia đối tia BM. Vậy D, B, M thẳng hàng.
a/
\(KD\perp AB\Rightarrow\widehat{CHB}=90^o\)
\(\widehat{AMB}=90^o\) (góc nội tiếp chắn nửa đường tròn)
=> M và H cùng nhìn Bc dưới 1 góc \(=90^o\) Nên M và H cùng nằm trên đường tròn đường kính AB nên B;M;H;C cùng nằm trên 1 đường tròn
b/
Ta có \(AB\perp KD\Rightarrow HK=HD\) (đường kính vuông góc với dây cung thì chia đôi dây cung)
Xét tam giác AKD có AH vừa là đường cao vừa là đường trung trực nên tg AKD là tg cân tại A => AK=AD
=> số đo cung AK = số đo cung AD (hai dây cung bằng nhau thì căng hai cung bằng nhau)
Ta có
số đo \(\widehat{KMA}=\frac{1}{2}\) số đo cung AK (góc nội tiếp đường tròn)
số đo \(\widehat{AKD}=\frac{1}{2}\) số đo cung AD (góc nội tiếp đường tròn)
Mà số đo cung AK = số đo cung AD (cmt)
\(\Rightarrow\widehat{KMA}=\widehat{AKD}\)
Xét tg AKC và tg AMK có
\(\widehat{KAM}\) chung
\(\widehat{AKD}=\widehat{AMK}\left(cmt\right)\)
=> tg AKC đồng dạng tg AMK (g.g.g) \(\Rightarrow\frac{AK}{AM}=\frac{AC}{AK}\Rightarrow AK^2=AC.AM\left(dpcm\right)\)
c/
Xét tg vuông AHC và tg vuông AMB có \(\widehat{MAB}\) chung => tg AHC đồng dạng tg AMB
\(\Rightarrow\frac{AH}{AM}=\frac{AC}{AB}\Rightarrow AH.AB=AC.AM=AK^2\)
\(\Rightarrow\frac{R}{2}.2R=AK^2=R^2\Rightarrow AK=R\)
Xét tg vuông AHK có
\(KH^2=AK^2-AH^2=R^2-\frac{R^2}{4}=\frac{3R^2}{4}\Rightarrow KH=\frac{R\sqrt{3}}{2}\)
\(KC=CH=\frac{KH}{2}=\frac{R\sqrt{3}}{4}\)
Xét tg vuông ACH có
\(AC^2=CH^2+AH^2=\frac{3R^2}{16}+\frac{R^2}{4}=\frac{7R^2}{16}\Rightarrow AC=\frac{R\sqrt{7}}{4}\)
Mà \(AK^2=AC.AM\Rightarrow AM=\frac{AK^2}{AC}=\frac{R^2}{\frac{R\sqrt{7}}{4}}=\frac{4R\sqrt{7}}{7}\)
Ta có \(CM=AM-AC=\frac{4R\sqrt{7}}{7}-\frac{R\sqrt{7}}{4}=\frac{9R\sqrt{7}}{28}\)
Xét tg vuông MEC và tg vuông AHC có \(\widehat{ECM}=\widehat{ACH}\) (góc đối đỉnh) => tg MEC đồng dạng tg AHC)
\(\Rightarrow\frac{CE}{AC}=\frac{MC}{CH}\Rightarrow CE=\frac{AC.MC}{CH}=\frac{\frac{R\sqrt{7}}{4}.\frac{9R\sqrt{7}}{28}}{\frac{R\sqrt{3}}{4}}=\frac{3R\sqrt{3}}{4}\)
d/ Giao đường tròn ngoại tiếp tg ACE là gia 3 đường trung trực
Ta có A cố định, K cố định nên đường trung trực của
Em tham khảo tại đây nhé.
Câu hỏi của Vũ Huy Hiệu - Toán lớp 9 - Học toán với OnlineMath
\(\text{a) Xét tứ giác ADMO có:}\)
∠DMO =90o (do M là tiếp tuyến của (O))
∠DAO =90o (do AD là tiếp tuyến của (O))
=> ∠DMO + ∠DAO = 180o
=> Tứ giác ADMO là tứ giác nội tiếp.
\(\text{b) Do D là giao điểm của 2 tiếp tuyến DM và DA nên OD là tia phân giác của ∠AOM}\)
=>(AOD = \(\frac{1}{2}\)∠AOM
Mặt khác ta có (ABM là góc nội tiếp chắn cung AM
=> ∠ABM = \(\frac{1}{2}\)∠AOM
=> ∠AOD = ∠ABM
Mà 2 góc này ở vị trí đồng vị
=> OD // BM
Xét tam giác ABN có:
OM// BM; O là trung điểm của AB
=> D là trung điểm của AN
c) Ta có: ΔOBM cân tại O ;OE ⊥MB =>OE là đường trung trực của MB
=>EM = EB => ΔMEB cân tại E => ∠EMB = ∠MEB (1)
ΔOBM cân tại O => ∠OMB = ∠OBM (2)
Cộng (1) và (2) vế với vế, ta được:
∠EMB + ∠OMB = ∠MEB + ∠OBM ⇔ ∠EMO =∠EOB ⇔ ∠EOB =90o
=>OB ⊥ BE
Vậy BE là tiếp tuyến của (O).
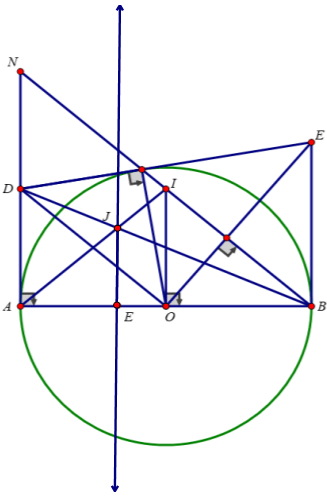
d) Lấy điểm E trên tia OA sao cho OE = \(\frac{OA}{3}\)
Xét tam giác OAI có OI vừa là đường cao vừa là trung tuyến
=> Tam giác OAI cân tại I => IA = IB; ∠IBA = ∠IAB
Ta có:
\(\hept{\begin{cases}\widehat{IBA}=\widehat{IAB}\\\widehat{IBA}+\widehat{INA}=90^0\\\widehat{NAI}+\widehat{IAB}=\widehat{NAB}=90^0\end{cases}}\)
=> ∠NAI = ∠INA => ΔINA cân tại I => IA = IN
Tam giác NAB vuông tại A có: IA = IN = IB
=> IA là trung tuyến của tam giác NAB
Xét ΔBNA có:
IA và BD là trung tuyến; IA ∩ BD = {J}
=> J là trọng tâm của tam giác BNA
Xét tam giác AIO có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}=\frac{2}{3}\Rightarrow\text{JE}\text{//}OI\)
=> J nằm trên đường thẳng d vuông góc với AB và cách O một khoảng bằng R/3.
Phần đảo: Lấy điểm J' bất kì thuộc đường thẳng d
Do d// OI (cùng vuông góc AB) nên ta có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}\)
\(\text{MÀ}\frac{AE}{AO}=\frac{2}{3}\Rightarrow\frac{\text{AJ}}{AI}=\frac{2}{3}\)
AI là trung tuyến của tam giác NAB
=> J' là trọng tâm tam giác NAB
Vậy khi M di chuyển trên (O) thì J di chuyển trên đường thẳng d vuông góc với AB và cách O một khoảng là R/3.
HÌNH Ở TRONG THỐNG KÊ HỎI ĐÁP NHA
