K
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 11 2021
Bài 2: ta thấy A và B ở vị trí trong cùng phía , A + B = 180 độ =>a//b(1)
Ta lại thấy B , C ở vị trí đồng vị , B=C=70 độ =>b//c(2)
Từ 1,2 =>a//b//c
H9
HT.Phong (9A5)
CTVHS
14 tháng 8 2023
a) Ta thấy:
\(\widehat{BED}+\widehat{EBC}=180^o\)
Mà hai góc này ở vị trí trong cùng phía
\(\Rightarrow DE//BC\)
b) Mà: DE//BC
\(\Rightarrow\widehat{EDC}+\widehat{BCD}=180^o\)(hai góc trong cùng phía)
\(\Rightarrow\widehat{EDC}=180^o-\widehat{BCD}=180^o-40^o=140^o\)
Ta lại có:
\(\widehat{EDC}\) đối đỉnh \(\widehat{xDC}\)
\(\Rightarrow\widehat{xDC}=\widehat{EDC}=140^o\)
KV
14 tháng 8 2023
a) Ta có:
∠BED + ∠EBC = 110⁰ + 70⁰ = 180⁰
Mà ∠BED và ∠EBC là hai góc trong cùng phía
⇒ DE // BC
b) Do DE // BC
⇒ ∠EDC + ∠DCB = 180⁰ (hai góc trong cùng phía)
⇒ ∠EDC = 180⁰ - ∠DCB
= 180⁰ - 40⁰
= 140⁰
Do DE // BC
⇒ ∠xDC = ∠DCB = 40⁰ (so le trong)
AM
9 tháng 2 2022
a. Xét \(\Delta ABD\) vuông tại A và \(\Delta HBD\) vuông tại H có: \(\left\{{}\begin{matrix}BD.là.cạnh.chung\\\widehat{ABD}=\widehat{HBD}\left(BD.là.tia.phân.giác.của.\widehat{ABC}\right)\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ABD\)=\(\Delta HBD\) (c-g) \(\Rightarrow\) DA=DH(đpcm) \(\Rightarrow\)BA=BH(đpcm)
c. Xét tứ giác ABHD có: \(\widehat{DAB}+\widehat{ABH}+\widehat{BHD}+\widehat{HDA}=360^o\)
\(\Leftrightarrow90^o+\widehat{ABH}+90^o+110^o=360^o\)
\(\Rightarrow\widehat{ABC}=\widehat{ABH}=70^o\Rightarrow\widehat{ACB}=90^o-70^o=20^o\) ,\(\widehat{A}=90^o\)
8 tháng 11 2021
ta có : a \(\perp\) P và b \(\perp\) Q \(\Rightarrow\)a//b
M1 và N1 là cặp góc trong cùng phía bù nhau
\(\Rightarrow\)M1= \(^{180^0}\)- N1= 180- \(65^0\)= 115
TL
1
5 tháng 8 2017
ko có hình vẽ bn ơi , nếu ko có thì các ko giải đc nha bn
29 tháng 5 2019
a) Có \(AB^2+AC^2=6^2+8^2=100\) ; \(BC^2=10^2=100\)
ta thấy \(AB^2+AC^2=BC^2=100\)
=> \(\Delta ABC\) vuông tại A
b) Xét \(\Delta ABM\)và \(\Delta NBM\) có:
\(\widehat{ABM}=\widehat{NBM};BM:chung;\widehat{BAM}=\widehat{BNM}\)
=> \(\Delta ABM\) = \(\Delta NBM\)
=> AM = MN
c) Xét \(\Delta AMP\) và \(\Delta NMC\)có :
\(\widehat{AMP}=\widehat{CMN};AM=NM;\widehat{PAM}=\widehat{CNM}=90^o\)
=> \(\Delta AMP\) = \(\Delta NMC\)
Xét \(\Delta AMP\) vuông tại A
=> MP > AM mà AM = MN
=> MP > MN
=
VM
29 tháng 5 2019
Hình bạn tự vẽ nha.
a) Ta có: AB2 + AC2 = 62 + 82 = 36 + 64 = 100
BC2 = 102 = 100
=> AB2 + AC2 = BC2 (=100)
Áp dụng định lí Py - ta - go đảo
=> ΔABC vuông tại A.
b) Xét 2 Δ vuông ABM và NBM có:
∠BAM = ∠BNM = 90 độ
Cạnh BM chung
∠B1 = ∠B2 (vì BM là tia phân giác của ∠B)
=> ΔABM = ΔNBM (cạnh huyền - góc nhọn)
=> AM = NM (2 cạnh tương ứng)
c) Xét 2 Δ vuông AMP và NMC có:
∠PAM = ∠CNM = 90 độ
AM = NM (cmt)
∠AMP = ∠CMN (vì 2 góc đối đỉnh)
=> ΔAMP = ΔNMC
+) Xét Δ PAM vuông tại A có:
∠PAM = 90 độ là góc lớn nhất
=> PM là cạnh lớn nhất
=> PM > AM
mà AM = MN (cmt)
=> PM > MN.
Chúc bạn học tốt!
7 tháng 5 2019
a.
Xét \(\Delta ABC\) có:
\(AB^2+AC^2=6^2+8^2=100=10^2\)
Theo định lý Pythagoras đảo thì \(\Delta ABC\) vuông tại A
b.
Xét \(\Delta ABM\) và \(\Delta NBM\) có:
\(\widehat{ABM}=\widehat{NBM}\)
BM là cạnh chung
\(\widehat{BAM}=\widehat{BNM}=90^0\)
\(\Rightarrow\Delta ABM=\Delta NBM\left(ch-gn\right)\Rightarrow MA=MN\)
c.
Xét \(\Delta PAM\) và \(\Delta CNM\) có:
\(MA=MN\)
\(\widehat{PAM}=\widehat{MNC}\)
\(\widehat{AMP}=\widehat{CMN}\)
\(\Rightarrow\Delta PAM=\Delta CNM\left(g.c.g\right)\Rightarrow MN=MP\)
Do \(\Delta MNC\) vuông tại N nên \(MC>MN\left(ch>cgv\right)\)
\(\Rightarrow MP>MN\)
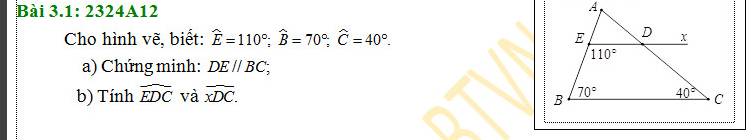
a, xét \(\Delta AMN\) có: góc ngoài của \(\Delta AMN\)tại góc M là 1100
\(\Rightarrow\widehat{AMN}=180^0-110^0=70^0\)
Có \(\widehat{AMN}=\widehat{MBC}\left(=70^0\right)\)mà chúng ở vị trí so le trong
\(\Rightarrow MN//BC\)
b,xét \(\Delta ABC\)có:
\(\widehat{BAC}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{BAC}=180^0-\left(70^0+65^0\right)\)
\(\Rightarrow\widehat{BAC}=45^0\)
Có \(M\in AB,N\in AC\)
\(\Rightarrow\widehat{BAC}=\widehat{MAN}=45^0\)