
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


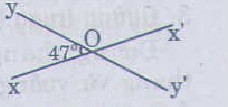
Giả sử hai đường thẳng xx' và yy' cắt nhau tại O và ˆxOy=47∘xOy^=47∘ (hình vẽ bên). Suy ra ˆx′Oy′=ˆxOy=47∘x′Oy′^=xOy^=47∘ (hai góc đối đỉnh).
ˆxOy′=180∘−ˆxOy=180∘−47∘=133∘xOy′^=180∘−xOy^=180∘−47∘=133∘ (do ˆx′Oyx′Oy^ và ˆxOy′xOy′^ kề bù)
Và ˆx′Oy=ˆxOy′=133∘x′Oy^=xOy′^=133∘ (hai góc đối đỉnh).

Giả sử hai đường thẳng xx' và yy' cắt nhau tại O và ˆxOy=47∘xOy^=47∘ (hình vẽ bên). Suy ra ˆx′Oy′=ˆxOy=47∘x′Oy′^=xOy^=47∘ (hai góc đối đỉnh).
ˆxOy′=180∘−ˆxOy=180∘−47∘=133∘xOy′^=180∘−xOy^=180∘−47∘=133∘ (do ˆx′Oyx′Oy^ và ˆxOy′xOy′^ kề bù)
Và ˆx′Oy=ˆxOy′=133∘x′Oy^=xOy′^=133∘ (hai góc đối đỉnh).

x y a b O 48
Vì xOb và xOa kề bù
\(\Rightarrow\widehat{xOb}+\widehat{xOa}=180^o\left(kb\right)\)
\(\Rightarrow48^o+\widehat{xOa}=180^o\Leftrightarrow\widehat{xOa}=180^o-48^o=132^o\)
Vì xOb và aOy đối đỉnh
\(\Rightarrow\widehat{xOb}=\widehat{aOy}=48^o\)
Vì xOa và yOb đổi đính
\(\Rightarrow\widehat{xOa}=\widehat{yOb}=132^o\)
các cậu còn lại tương tự

1. x O x' y y'
Giải: a) Ta có: \(\widehat{xOy}+\widehat{yOx'}=180^0\) (kề bù)
=> \(\widehat{yOx'}=180^0-\widehat{xOy}=180^0-75^0=105^0\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOy}=75^0\) => \(\widehat{x'Oy'}=75^0\)
\(\widehat{yOx'}=\widehat{xOy'}\) (đối đỉnh)
Mà \(\widehat{yOx'}=105^0\) => \(\widehat{xOy'}=105^0\)
1b) Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\) (kề bù)
mà \(\widehat{x'Oy}-\widehat{xOy}=30^0\)
=> \(2.\widehat{x'Oy}=210^0\)
=> \(\widehat{x'Oy}=210^0:2=105^0\) => \(\widehat{x'Oy}=\widehat{xOy'}=105^0\) (đối đỉnh)
=> \(\widehat{xOy}=180^0-105^0=75^0\) => \(\widehat{xOy}=\widehat{x'Oy'}=75^0\) (đối đỉnh)
2. O x y x' y' m m'
Giải: a) Ta có: \(\widehat{xOm}=\widehat{x'Om'}\) (đối đỉnh)
\(\widehat{mOy}=\widehat{m'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}\) (gt)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}.\widehat{xOy}\) (vì Om là tia p/giác)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}=\frac{1}{2}.\widehat{xOy}\)
=> Om' nằm giữa Ox' và Oy'
=> Om' là tia p/giác của góc x'Oy'
b) Tự viết