Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ∆ABC có :
BAC + ACB + ABC = 180°
=> ABC + ACB = 180° - 90° = 90°
Xét ∆ABH có :
BAH + BHA + ABH = 180°
=> ABH + BAH = 90°
Xét ∆AHC ta có :
AHC + HCA + HAC = 180°
=> HAC + HCA = 90°
=> BAH = HAC
=> AH là phân giác BAC
Mà AH là đường cao
=> ∆ABC cân tại A
=> ABC = ACB
Hay ABH = C , ACH = B

a) Xét ∆DIC và ∆DAC ta có :
DC chung
CI = CA
ICD = ACD ( CD là phân giác)
=> ∆DIC = ∆DAC (c.g.c)
=> DA = DI ( tương ứng)
b) Vì ∆DIC = ∆DAC (cmt)
=> DAC = DIC = 90°
c) Ta có : IC = AC (gt)
=> ∆IAC cân tại C
Mà CD là phân giác ∆BCA
=> CD là trung trực ∆AIC
=> CD \(\perp\)AI

B A C E D
a, Vì BA = BC => \(\Delta ABC\) cân tại B => \(\widehat{A}=\widehat{C}\)
b, Vì BA = BC => BE = BD
Xét \(\Delta BDA\) và \(\Delta BEC\) có:
BA = BC (gt)
BD = BE (cmt)
\(\widehat{B}\): chung
Do đó \(\Delta BDA=\Delta BEC\left(c.g.c\right)\)
=> \(\widehat{BDA}=\widehat{BEC}\) (2 góc t/ứ)
c, Vì \(\Delta BDA=\Delta BEC\Rightarrow\widehat{BAD}=\widehat{BCE}\) (2 góc tương ứng)
Mà \(\widehat{A}=\widehat{C}\) (câu a)
Do đó \(\widehat{A}-\widehat{BAD}=\widehat{C}-\widehat{BCE}\) hay \(\widehat{CAD}=\widehat{ACE}\)

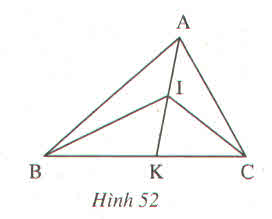
a)Ta có \(\widehat{BIK}\) là góc ngoài của BAI.
Nên \(\widehat{BIK}>\widehat{BAI}\) (1)
b) \(\widehat{CIK}>\widehat{CAI}\)( Góc ngoài của \(\Delta\) CAI)
Từ (1) và (2) ta có:
\(\widehat{BIK}+\widehat{CIK}>\widehat{BAI}+\widehat{CAI}\)
\(\Rightarrow\widehat{BIC}>\widehat{BAC}\)
) Ta có ∠BIK là góc ngoài của ∠BAI( hay là góc ngoài ∠BAK)
Các em lưu ý nếu không hiểu: Góc ngoài của tam giác lớn hơn mỗi ngóc trong không kề với nó (ở đây là tam giác ∆ BIA)
Nên ∠BIK > ∠BAK (1)
b) Góc ∠CIK > ∠CAI (2) (Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có: ∠BIK + ∠CIK > ∠BAK + ∠CAI
Mà ∠BIC = ∠BIK + ∠CIK; ∠BAC = ∠BAK + ∠CAI
⇒ ∠BIC > ∠BAC.

B C A I 1 1 2 2 M
a) xét \(\Delta ABC\)CÓ
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow80^o+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=100^o\)
mà hai tia BI và CI lần lượt là tia hân giác của ^B và ^C
\(\Rightarrow\widehat{B_1}+\widehat{B_2}+\widehat{C_1}+\widehat{C_2}=100^o\)
\(\Rightarrow2\widehat{B_2}+2\widehat{C_2}=100^o\)
\(\Rightarrow2\left(\widehat{B_2}+\widehat{C_2}\right)=100^o\)
\(\Rightarrow\widehat{B_2}+\widehat{C_2}=50^o\)
XÉT \(\Delta BCI\)Có
\(\widehat{B_2}+\widehat{C_2}+\widehat{BIC}=180^o\left(đl\right)\)
THAY \(50^o+\widehat{BIC}=180^o\)
\(\Rightarrow\widehat{BIC}=180^o-50^o=130^o\)
B) TA CÓ
\(\widehat{BIC}=130^o;\widehat{BAC}=80^o\)
\(\Rightarrow\widehat{BIC}>\widehat{BAC}\left(1\right)\left(130^o>80^o\right)\)
mà \(\widehat{BIC}>\widehat{BMC}\left(2\right)\)( Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó.)
MÀ \(\widehat{BAM}< \widehat{BMC}\)HAY \(\widehat{BAC}< \widehat{BMC}\left(3\right)\)( Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó.)
TỪ (1) VÀ (2) VÀ (3) \(\Rightarrow\widehat{BIC}>\widehat{BMC}>\widehat{BAC}\)