
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


có ABCD là Hthang vuông (gt)
=> AB // CD (t/c Hthang)
mà E thuộc CD => AB // EC
tứ giác ABCE có AB // EC (cmt)
AE // BC ( gt)
=> ABCE là HBH ( vì là tứ giác có các cạnh đối //)
=> AB = EC = 16 ( t/c HBH )
AE = BC = 17
có DE + EC = DC
=> DE + 16 = 24
=> DE = 8
có tam giác ADE vuông tại D ( vì ABCD là Hthang vuông)
=> \(AD^2+DE^2=AE^2\) (định lý Py-ta-go)
=>\(AD^2=AE^2-DE^2=17^2-8^2\)
= 225 = \(15^2\)
=>AD =15

a: \(CB=\sqrt{12^2+16^2}=20\left(cm\right)\)
AH=12*16/20=9,6cm
Xet ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=20/7
=>BD=60/7cm; CD=80/7cm
b: Sửa đề: AB,AC
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
AM=AH^2/AB=9,6^2/12=7,68(cm)
AN=AH^2/AC=9,6^2/16=5,76(cm)
\(S_{AMHN}=7.68\cdot5.76=44.2368\left(cm^2\right)\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 12^2+16^2=20cm
AH=12*16/20=9,6cm
BH=AB^2/BC=7,2cm
c: AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=20/7
=>BD=60/7\(\simeq8,6\left(cm\right)\) và CD=80/7\(\simeq11,4\left(cm\right)\)

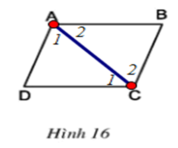
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
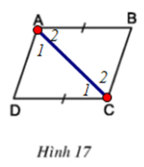
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)

Bạn tự vẽ hình nha ==''
a.
AB _I_ BC
AB _I_ AD
=> AD // BC
b.
AD // BC
=> C + D = 1800 (2 góc kề bù)
\(C=3D\Rightarrow\frac{C}{3}=\frac{D}{1}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{C}{3}=\frac{D}{1}=\frac{C+D}{3+1}=\frac{180^0}{4}=45^0\)
\(\frac{C}{3}=45^0\Rightarrow C=45^0\times3=135^0\)
\(\frac{D}{1}=45^0\Rightarrow D=45^0\)
Chúc bạn học tốt ^^

hình bạn tự vé nhé.
tam giác ABC vuông tại A nên theo định lý PY-Ta-Go ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow6^2+8^2=BC^2\)
\(\Rightarrow BC=10\left(DO-BC>0\right)\)
b) xét \(\Delta ABC\) VÀ \(\Delta HBA\) CÓ:
\(\widehat{BAC}=\widehat{AHB}\)
\(\widehat{B}\) CHUNG
\(\Rightarrow\Delta ABC\) đồng dạng vs \(\Delta HBA\)
c)sửa đề:\(AB^2=BH.BC\)
TA CÓ: \(\Delta ABC\text{ᔕ}\Delta HBA\)
\(\Rightarrow\frac{AB}{BH}=\frac{BC}{AB}\left(tsđd\right)\)
\(\Rightarrow AH^2=BH.BC\)

a) Xét ΔABC vuông tại A có \(\widehat{C}=30^0\)(gt)
mà cạnh đối diện với \(\widehat{C}\)
nên \(\dfrac{AB}{BC}=\dfrac{1}{2}\)(Định lí)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AD}{CD}=\dfrac{1}{2}\)
b) Ta có: \(BC=2\cdot AB\)(cmt)
nên \(BC=2\cdot12.5=25\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=25^2-12.5^2=468.75\)
hay \(AC=\dfrac{25\sqrt{3}}{2}cm\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{12\cdot\dfrac{25\sqrt{3}}{2}}{2}=\dfrac{150\sqrt{3}}{2}=75\sqrt{3}\left(cm^2\right)\)
AD=15 cm
Dựa vào tính chất pitago