Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
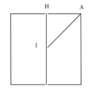
Thiết diện qua trục hình trụ là hình vuông → chiều cao h = 2R = 2
Trung điểm I của trục hình trụ là tâm khối cầu ngoại tiếp hình trụ, bán kinh là IA.
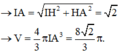

Đáp án A
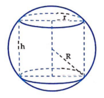
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là r và h. Khi đó thiết diện qua trục của hình trụ là một hình chữ nhật có kích thước hai cạnh là 2r và h. Diện tích hình chữ nhật đó là S = 2 r h .
Quan sát hình vẽ, ta thấy R 2 = h 2 2 + r 2 ⇔ h = 2 R 2 − r 2 = 2 3 a 2 − r 2 .
Khi đó S = 2 r h = 4 r 3 a 2 − r 2 ≤ 4. r 2 + 3 a 2 − r 2 2 2 = 6 a 2 . Dấu “=” xảy ra khi và chỉ khi
r = 3 a 2 − r 2 ⇔ 2 r 2 = 3 a 2 ⇔ r = a 6 2 ⇒ h = 2 3 a 2 − 3 a 2 2 = a 6
Vậy diện tích toàn phần của hình trụ (T) là
S t p = 2 π r h + 2 π r 2 = 2 π a 6 . a 6 2 + 2 π a 6 2 2 = 9 π a 2 (đvdt).

Đáp án C.
ABCD là hình vuông với DC=2R=4cm từ đó Ad=4cm
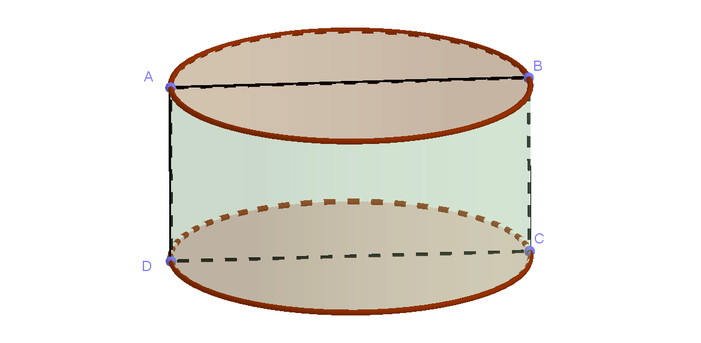
Từ đó: V H i n h = S d a y . A D = π 2 2 .4 = 16 π c m 2 .

Đáp án là A
Thiết diện qua trục là hình vuông nên hình trụ có chiều cao h là độ dài cạnh bên và bằng 2 lần bán kính đáy R.
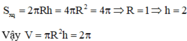
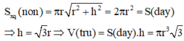

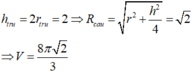


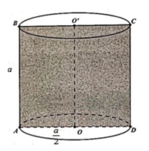
Ta có:
V 1 V 2 = π a 2 2 a 4 3 π a 2 2 3 = 3 2 8
Đáp án D