K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\Rightarrow OH\perp\left(ABCD\right)\)
\(\Rightarrow V_{O.ABCD}=\dfrac{1}{3}OH.S_{ABCD}\)
Đặt \(OH=x\Rightarrow BH=\sqrt{R^2-OH^2}=\sqrt{9a^2-x^2}\)
\(\Rightarrow AB=2BH=2\sqrt{9a^2-x^2}\)
\(\Rightarrow V=\dfrac{1}{3}x.3a.2\sqrt{9a^2-x^2}=a.2x.\sqrt{9a^2-x^2}\le a\left(x^2+9a^2-x^2\right)=9a^3\)
\(\Rightarrow V_{max}=9a^3\)

CM
7 tháng 7 2018
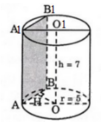
Mặt phẳng (P) song song với trục và cách trục 3cm, cắt hình trụ theo thiết diện là tứ giác A A 1 B 1 B .
Gọi H là trung điểm của AB.
Ta có 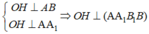

SAA1B1B = AB. AA1 = 8. 7 = 56 (cm2)
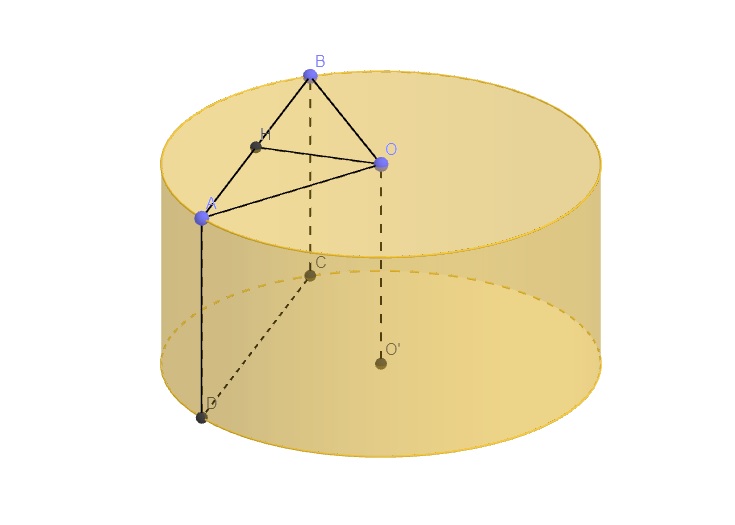
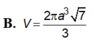

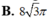

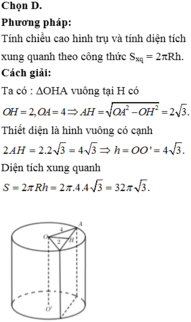


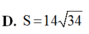

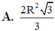
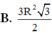

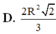

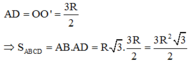

Hạ \(OH\perp AB\) tại H. Theo đề bài, ta thấy ngay \(\widehat{OAH}=30^o\). Lại có \(OA=\dfrac{OH}{\sin OAH}=\dfrac{\dfrac{10a}{3}}{\dfrac{1}{2}}=\dfrac{20a}{3}\)
Mặt khác, \(AH=OA.\cos OAH=\dfrac{20a}{3}.\dfrac{\sqrt{3}}{2}=\dfrac{10a\sqrt{3}}{3}\). Từ đó suy ra \(AB=2AH=2.\dfrac{10a\sqrt{3}}{3}=\dfrac{20a\sqrt{3}}{3}\)
Do ABCD là hình vuông nên \(AB=BC=\dfrac{20a\sqrt{3}}{3}\)
Vậy thể tích hình trụ đã cho là \(V_{trụ}=\pi.OA^2.BC=\pi.\left(\dfrac{20a}{3}\right)^2.\dfrac{20a\sqrt{3}}{3}\) \(=\dfrac{8000\sqrt{3}}{27}.\pi.a^3\) (đvdt)